Bài tập 1 trang 169 Tài liệu dạy – học Toán 8 tập 1, Cho hình thoi ABCD có AC =12 cm, BD = 9 cm. Gọi M, N, p, Q lần lượt là trung điếm của các cạnh AB, BC, CD, DA....

Cho hình thoi ABCD có AC =12 cm, BD = 9 cm. Gọi M, N, p, Q lần lượt là trung điếm của các cạnh AB, BC, CD, DA.

a) Tứ giác MNPQ là hinh gì ?

b) Tính diện tích tứ giác MNPQ.

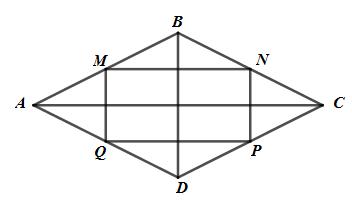
a) N, P lần lượt là trung điểm của BC và CD (gt)

$\Rightarrow NP$ là đường trung bình của tam giác BCD

$\Rightarrow NP//BD$ và $NP = {1 \over 2}BD\,\,\left( 1 \right)$

M, Q lần lượt là trung điểm của AB và AD (gt)

$\Rightarrow MQ$ là đường trung bình của tam giác ABD

$\Rightarrow MQ//BD$ và $MQ = {1 \over 2}BD\,\,\left( 2 \right)$

Từ (1) và (2) $\Rightarrow MQ//NP$ và $MQ = NP$

Do đó tứ giác MNPQ là hình bình hành.

Ta có $MQ//BD$ và $AC \bot BD$ (ABCD là hình thoi)

$\Rightarrow MQ \bot AC$

Mà $QP//AC$ (QP là đường trung bình của tam giác ACD) $\Rightarrow MQ \bot QP$

Nên tứ giác MNPQ là hình chữ nhật.

b) $MQ = {{BD} \over 2} = {9 \over 2} = 4,5\,\,\left( {cm} \right)$

$QP = {{AC} \over 2}$  (QP là đường trung bình của tam giác ACD)

$\Rightarrow QP = {{12} \over 2} = 6\,\,\left( {cm} \right)$

Diện tích hình chữ nhật MNPQ là : $MQ.QP = 4,5.6 = 27\,\,\left( {c{m^2}} \right)$