
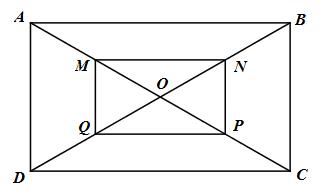
Cho hình chữ nhật ABCD có tâm O và trung điểm các đoạn OA, OB, OC, OD lản lượt là M, N, P, Q.
a) Chứng minh rủng tứ giác MNPQ là hình chữ nhật.
b) Cho biết diện tích MNPQ bằng 20 m2. Tính diện tích hình chữ nhật ABCD.

a) O là tâm đối xứng của hình chữ nhật ABCD (gt) \( \Rightarrow OA = OB = OC = OD\)
Mà M, N, P, Q là trung điểm của OA, OB, OC, OD (gt)
\( \Rightarrow OM = ON = OP = OQ\)
\( \Rightarrow O\) là trung điểm của MP và NQ.
Do đó tứ giác MNPQ là hình bình hành.
Advertisements (Quảng cáo)
Mà \(MP = QN\) (vì \(MO + OP = QO + ON\))
Nên MNPQ là hình chữ nhật.
b) M, N lần lượt là trung điểm của OA, OB (gt)
\( \Rightarrow MN\) là đường trung bình của tam giác OAB \( \Rightarrow MN = {{AB} \over 2}\)
N, P lần lượt là trung điểm của OB, OC (gt)
\( \Rightarrow NP\) là đường trung bình của tam giác OBC \( \Rightarrow NP = {{BC} \over 2}\)
\({S_{MNPQ}} = MN.NP \Rightarrow 20 = MN.NP\)
Mà \(\left\{ \matrix{ MN = {{AB} \over 2} \hfill \cr NP = {{BC} \over 2} \hfill \cr} \right.\)
Nên \(20 = {{AB} \over 2}.{{BC} \over 2} \Rightarrow AB.BC = 20.4 = 80 \Rightarrow S = 80\,\,\left( {c{m^2}} \right)\)
