Bài tập 11 trang 134 Tài liệu dạy – học Toán 8 tập 1, Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA và I, K lần lượt là trung điểm các đường...

Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA và I , K lần lượt là trung điểm các đường chép AC và BD. Chứng minh:

a) Các tứ giác MNPQ, INKQ là hình bình hành.

b) Các đường thẳng MP, NQ, IK đồng quy.

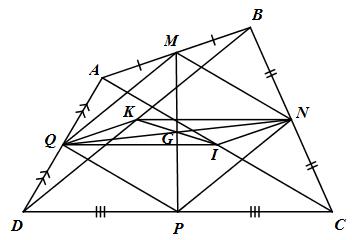
a) Gọi M, N lần lượt là trung điểm của AB, BC

$\Rightarrow MN$ là đường trung bình của tam giác ABC $\Rightarrow MN//AC$ và $MN = {1 \over 2}AC\,\,\,\left( 1 \right)$

Q, P là trung điểm của AD và DC

$\Rightarrow QP$ là đường trung bình của tam giác ADC $\Rightarrow QP//AC$ và $QP = {1 \over 2}AC\,\,\,\left( 2 \right)$

Từ (1) và (2) suy ra $MN//QP$ và $MN = QP$

$\Rightarrow MNPQ$ là hình bình hành (dấu hiệu nhận biết)

Ta có: Q, I lần lượt là trung điểm của AC và AC

$\Rightarrow QI$ là đường trung bình của tam giác ADC $\Rightarrow QI//DC$ và $QI = {1 \over 2}DC\,\,\,\left( 3 \right)$

K, N lần lượt là trung điểm của DB và BC

$\Rightarrow KN$ là đường trung bình của tam giác DBC

$\Rightarrow KN//DC$ và $KN = {1 \over 2}DC\,\,\left( 4 \right)$

Từ (3) và (4) suy ra $QI//KN$ và \(QI = KN\(.

$\Rightarrow INKQ$ là hình bình hành (dấu hiệu nhận biết)

b) Gọi G là giao điểm của MP và NQ (5)

Mà MP và NQ là hai đường chéo của hình bình hành MNPQ

Nên G là trung điểm của QN

Tứ giác INKQ là hình bình hành có G là trung điểm của QN

$\Rightarrow G$ là trung điểm của IK $\Rightarrow IK$ đi qua G (6)

Từ (5), (6) suy ra MP, NQ, IK đồng quy.