
Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tái phân giác của góc B cắt CD ở F.
a) Chứng minh rằng DE // BF.
b) Tứ giác DEBF là hình gì ?
c) Chứng minh rằng ba đường thẳng AC, BD và EF đồng quy.

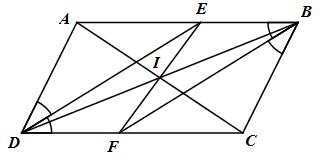
a) Ta có \(\widehat {ABC} = \widehat {ADC}\) (tứ giác ABCD là hình bình hành)
\(\widehat {ABF} = \widehat {{{ABC} \over 2}}\) (BF là tia phân giác của \(\widehat {ABC}\) ) và \(\widehat {CDE} = {{\widehat {ADC}} \over 2}\) (DE là tia phân giác của \(\widehat {ADC}\))
\( \Rightarrow \widehat {ABF} = \widehat {CDE}\)
Mà \(\widehat {ADE} = \widehat {CDE}\) (hai góc so le trong và AB // CD)
Nên \(\widehat {ABF} = \widehat {AED}\).
Advertisements (Quảng cáo)
Lại có \(\widehat {ABF}\) và \(\widehat {AED}\) là hai góc đồng vih
\( \Rightarrow DE//BF\).
b) Tứ giác DEBF có DE // BF và EB // DF (AB // CD)
Do đó tứ giác DEBF là hình bình hành (dấu hiệu nhận biết)
c) Gọi I là giao điểm của AC và BD (1)
Mà AC, BD là hai đường chéo của hình bình hành ABCD
Nên I là trung điểm của AC và BD.
Hình bình hành DEBF có I là trung điểm của BD nên I là trung điểm của EF.
\( \Rightarrow EF\) qua I (2)
Từ (1) và (2) ta có AC, BD và EF đồng quy tại I.
