
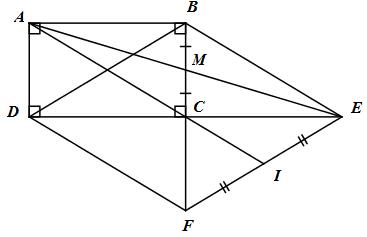
Cho hình chữ nhật ABCD, gọi M là trung điểm của BC và E là giao điểm của đường thẳng AM với đường thẳng DC.
a) Chứng minh rằng tứ giác ABEC là hình bình hành.
b) Gọi F là điểm đối xứng của B qua C. CHứng minh rằng tứ giác BEFD là hình thoi.
c) Gọi I là trung điểm của cạnh EF. Chứng minh rằng ba điểm A, C, I thẳng hàng.

a) Xét tam giác ABM và tam giác MCE có:
\(BM = MC\) (M là trung điểm của BC)
\(\widehat {ABM} = \widehat {MCE}\,\,\left( { = {{90}^0}} \right)\)
\(\widehat {BMA} = \widehat {CME}\) (hai góc đối đỉnh)
Do đó \(\Delta ABM = \Delta ECM\,\,\left( {g.c.g} \right) \Rightarrow AM = EM\) (hai cạnh tương ứng)
\( \Rightarrow M\) là trung điểm của AE.
Tứ giác ABEC có:
BC và AE cắt nhau tại M (gt) ;
M là trung điểm của BC (gt)
Advertisements (Quảng cáo)
M là trung điểm của AE (cmt)
Do đó tứ giác ABEC là hình bình hành.
b) Ta có \(CE = CD\,\,\left( { = AB} \right)\)
Tứ giác DBEF có :
DE và BF cắt nhau tại C (gt)
C là trung điểm của DE (cmt)
C là trung điểm của BF (F đối xứng với B qua C)
Do đó tứ giác DBEF là hình bình hành.
Mà \(DE \bot BF\,\,\left( {BC \bot DC;\,\,E \in DC;\,\,F \in BC} \right)\) nên tứ giác BDEF là hình thoi.
c) C, I lần lượt là trung điểm của BF và EF
\( \Rightarrow CI\) là đường trung bình của tam giác BEF \( \Rightarrow CI//BE\)
Mà \(CA//BE\) (tứ giác ABEC là hình bình hành)
Nên CI, CA trùng nhau (Tiên đề Ơ-clit)
Vậy ba điểm C, I, A thẳng hàng.
