
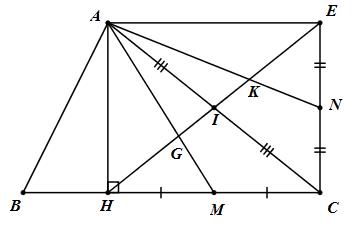
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.
a) Chứng minh rằng tứ giác AHCE là hình chữ nhật.
b) Chứng minh rằng I là trung điểm GK.
c) Góc C bằng bao nhiêu độ để tứ giác AHCE trở thành hình vuông.

a) Tứ giác AHCE có:
Hai đường chéo AC và HE cắt nhau tại I (gt);
I là trung điểm của AC (gt);
I là trung điểm của HE (E đối xứng với H qua I)
Do đó tứ giác AHCE là hình bình hành.
Mà \(\widehat {AHC} = {90^0}\) (AH là đường cao của tam giác ABC).
Advertisements (Quảng cáo)
Vậy tứ giác AHCE là hình chữ nhật.
b) Tam giác AHC có hai đường trung tuyến AM và HI cắt nhau tại G.
\( \Rightarrow G\) là trọng tâm của tam giác AHC \( \Rightarrow GI = {1 \over 3}HI\)
Tam giác AEC có hai đường trung tuyến AN và EI cắt nhau tại K.
\( \Rightarrow K\) là trọng tâm của tam giác AEC \( \Rightarrow IK = {1 \over 3}IE\)
Mà \(IE = HI\) (E đối xứng với H qua I)
\( \Rightarrow IK = GI \Rightarrow I\) là trung điểm của GK \(\left( {I \in GK} \right)\)
c) Nếu AHCE là hình vuông thì ta có :
CA là tia phân giác của góc vuông HCE.
\(\widehat {AHC} = {{{{90}^0}} \over 2} = {45^0}\)
Vậy \(\widehat C = {45^0}\) thì tứ giác AHCE trở thành hình vuông.
