
Cho hình 68. Chứng minh rằng tứ giác EFGH là hình thoi.
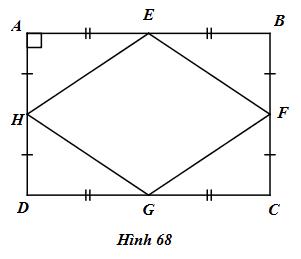

E, F lần lượt là trung điểm của AB và BC
\( \Rightarrow EF\) là đường trung bình của tam giác ABC
\( \Rightarrow EF//AC\) và \(EF = {1 \over 2}AC\,\,\,\left( 1 \right)\)
H, G lần lượt là trung điểm của AD và DC
\( \Rightarrow HG\) là đường trung bình của tam giác ACD
Advertisements (Quảng cáo)
\( \Rightarrow HG//AC\) và \(HG = {1 \over 2}AC\) (2)
Từ (1) và (2) \( \Rightarrow EF//HG\) và \(EF = HG\).
Vậy tứ giác EFGH là hình bình hành.
Tứ giác ABCD có \(AB = CD\) và \(AD = BC \Rightarrow \) Tứ giác ABCD là hình bình hành.
Mà \(\widehat {BAD} = {90^0} \Rightarrow ABCD\) là hình chữ nhật.
Xét \(\Delta EBF\) và \(\Delta CGF\) có :
\(\eqalign{ & EB = EC\,\,\left( {gt} \right) \cr & BF = FC\,\,\left( {gt} \right) \cr & \widehat {EBF} = \widehat {GCF}\,\,\left( { = {{90}^0}} \right) \cr & \Rightarrow \Delta EBF = \Delta GCF\,\,\left( {c.g.c} \right) \Rightarrow EF = GF \cr} \)
Chứng minh tương tự ta có \(GF = GH,\,\,GH = EF \Rightarrow EF = GF = GH = EH\)
Do đó tứ giác EFGH là hình thoi.
