Bài tập 6 trang 173 Tài liệu dạy – học Toán 8 tập 1, Cho hình thang ABCD (AB // CD). Gọi M. N, O lần lượt là trung điểm cùa AD, BC và MN. Qua O vẽ một dường thẳng cắt hai đáy AB và CD...

Cho hình thang ABCD (AB // CD). Gọi M. N, O lần lượt là trung điểm cùa AD, BC và MN. Qua O vẽ một dường thẳng cắt hai đáy AB và CD tại P và Q. Chứng minh hai tứ giác APQD và BCQP có diện tích bằng nhau.

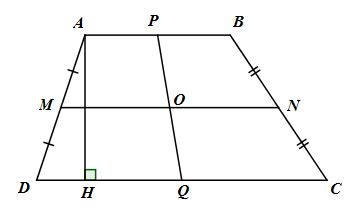
Tứ giác APQD có AP // DQ (AB // CD, $P \in AB,\,\,Q \in CD$)

$\Rightarrow$ Tứ giác APQD là hình thang

M, N lần lượt là trung điểm của AD và BC (gt)

$\Rightarrow MN$ là đường trung bình của hình thang ABCD $\Rightarrow MN//AB//CD$

Hình thang APQD có AP // MO // DQ

(MN // AB // CD, $P \in AB,\,\,Q \in CD,\,\,O \in MN$)

Và M là trung điểm của AD

$\Rightarrow O$ là trung điểm của PQ

Do đó MO là đường trung bình của hình thang APQD $\Rightarrow MO = {{AP + DQ} \over 2}$

Kẻ $AH \bot CD$ tại H

${S_{APQD}} = {1 \over 2}AH\left( {AP + DQ} \right) = AH.{{AP + DQ} \over 2} = AH.MO$

Chứng minh tương tự: ${S_{PBCQ}} = AH.ON$

Mà $MO = ON$ (O là trung điểm của MN) nên $S = {S_{PBCQ}}$