
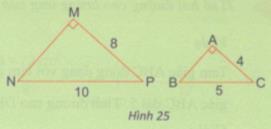
Cho hai tam giác vuông MNP và ABC có kích thước như hình 25. Tính các tỉ số \({{AC} \over {MP}}\) và \({{AB} \over {MN}}\) . Tam giác MNP có đồng dạng với tam giác ABC không ? Vì sao ?

\({{AC} \over {MP}} = {4 \over 8} = {1 \over 2}\)
∆MNP vuông tại M \( \Rightarrow M{N^2} + M{P^2} = N{P^2}\) (định lí Py-ta-go)
Do đó \(M{N^2} = N{P^2} - M{P^2} \) \(= {10^2} - {8^2} = 36,\)
\(MN > 0 \Rightarrow MN = \sqrt {36} = 6\)
Advertisements (Quảng cáo)
∆ABC vuông tại A \( \Rightarrow A{B^2} + A{C^2} = B{C^2}\) (định lí Py-ta-go)
\( \Rightarrow A{B^2} = B{C^2} - A{C^2} = {5^2} - {4^2} = 9\)
\(AB > 0 \Rightarrow AB = \sqrt 9 = 3\)
Ta có \({{AB} \over {MN}} = {3 \over 6} = {1 \over 2}\)
Xét ∆ABC và ∆MNP có \({{AB} \over {MN}} = {{AC} \over {MP}},\widehat A = \widehat M( = 90^\circ ) \)
\(\Rightarrow \Delta ABC \sim \Delta MNP(c.g.c)\)
