Luyện tập - Chủ đề 4 : Diện tích đa giác - Luyện tập 7 trang 172 Tài liệu dạy – học Toán 8 tập 1. Giải bài tập Chứng minh rằng tổng hai khoảng cách từ một điềm trên cạnh đáy của một tam giác cân đến hai cạnh bên luôn bẳng chiều cao ứng với cạnh bên.
Chứng minh rằng tổng hai khoảng cách từ một điềm trên cạnh đáy của một tam giác cân đến hai cạnh bên luôn bẳng chiều cao ứng với cạnh bên.
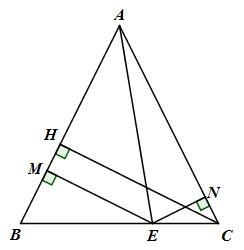
Kẻ \(EM \bot AB\) tại M, \(EN \bot AC\) tại N
\(EM + EN\) là tổng hai khoảng cách cần xét.
Advertisements (Quảng cáo)
Ta có: \({S_{ABC}} = {S_{ABE}} + {S_{ACE}} = {1 \over 2}AB.ME + {1 \over 2}C.NE\)
Mà \(AB = AC\,\,(\Delta ABC\) cân tại A)
Nên \({S_{ABC}} = {1 \over 2}AB.ME + {1 \over 2}AB.NE = {1 \over 2}AB\left( {ME + NE} \right)\)
Mặt khác \({S_{ABC}} = {1 \over 2}AB.CH\)
Do đó \({1 \over 2}AB\left( {ME + NE} \right) = {1 \over 2}AB.CH \Rightarrow ME + NE = CH\)