Bài 16. Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng. Bài 16 trang 67 - Sách giáo khoa toán 8 tập 2 - Tính chất đường phân giác của tam giác
Bài 16. Tam giác ABC có độ dài các cạnh AB= m, AC= n và AD là đường phân giác. Chứng minh rẳng tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng \(\frac{m}{n}\).
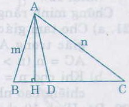

Kẻ AH ⊥ BC
Ta có:
SABD = \(\frac{1}{2}\)AH.BD
Advertisements (Quảng cáo)
SADC = \(\frac{1}{2}\)AH.DC
=>\(\frac{S_{SBD}}{S_{ADC}}\) = \(\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}\) = \(\frac{BD}{DC}\)
Mặt khác: AD là đường phân giác của ∆ABC
=> \(\frac{BD}{DC}\)= \(\frac{AB}{AC}\) = \(\frac{m}{n}\).
Vậy \(\frac{S_{SBD}}{S_{ADC}}\) = \(\frac{m}{n}\)
