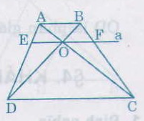
Bài 20. Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhat tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC théo thứ tự E và F(h26). Bài 20 trang 68 - Sách giáo khoa toán 8 tập 2 - Tính chất đường phân giác của tam giác
Bài 20. Cho hình thang ABCD (AB //CD). Hai đường chéo AC và BD cắt nhat tại O. Đường thẳng A qua O và song song với đáy của hình thang cắt các cạnh AD, BC théo thứ tự E và F(h26)
Chứng minh rằng OE = OF.

Advertisements (Quảng cáo)
∆ADC có OE // OC nên \(\frac{OE}{DC}\) = \(\frac{AE}{AD}\)
∆BDC có OF // DC nên \(\frac{OF}{DC}\) = \(\frac{BF}{BC}\)
Mà AB // CD => \(\frac{AE}{AD}\) = \(\frac{BF}{BC}\)(câu b bài 19)
Vậy \(\frac{OE}{DC}\) = \(\frac{OF}{DC}\) nên OE = OF.
