Bài 19. Cho hình thang ABCD (AB // CD).
Đường thẳng a song song với DC, cắt các cạnh AD và BC theo thứ tự là E và F.
Chứng minh rằng:
a) \(\frac{AE}{ED}\) = \(\frac{BF}{FC}\); b) \(\frac{AE}{AD}\) = \(\frac{BF}{BC}\) c) \(\frac{DE}{DA}\) = \(\frac{CF}{CB}\).

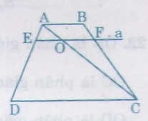
a) Nối AC cắt EF tại O
Advertisements (Quảng cáo)
∆ADC có EO // DC => \(\frac{AE}{ED}\) = \(\frac{AO}{OC}\) (1)
∆ABC có OF // AB => \(\frac{AO}{OC}\) = \(\frac{BF}{FC}\) (2)
Từ 1 và 2 => \(\frac{AE}{ED}\) = \(\frac{BF}{FC}\)
b) Từ \(\frac{AE}{ED}\) = \(\frac{BF}{FC}\) => \(\frac{AE}{ED +AE}\)= \(\frac{BF}{FC + BF}\)
hay \(\frac{AE}{AD}\)=\(\frac{BF}{BC}\)
c) Từ \(\frac{AE}{ED}\) = \(\frac{BF}{FC}\) => \(\frac{AE+ED}{ED}\)= \(\frac{BF+FC}{FC}\)
=> \(\frac{AD}{ED}\) = \(\frac{BF}{FC}\) hay \(\frac{ED}{AD}\) = \(\frac{FC}{BC}\)
