Bài 21. a) Cho tam giác ABC với đường trung tuyến AM và đường phân giác AD. Tính diện tích tam giác ADM, biết AB= m, AC= n( n>m). Và diện tích của tam giác ABC là S.
b) Cho n = 7cm, m = 3cm. Hỏi diện tích tam giác ADM chiếm bao nhiêu phần trăm diện tích tam giác ABC.
Giải:
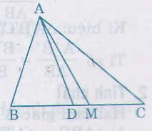
Ta có AD là đường phân giác của ∆ ABC nên
\(\frac{S_{ABD}}{S_{ADC}}\) = \(\frac{AB}{AC}\) = \(\frac{m}{n}\)(kết quả ở bài 16)
Advertisements (Quảng cáo)
=> \(\frac{S_{ABD}}{S_{ADC}+S_{ABD}}\)= \(\frac{m}{n+m}\)
hay \(\frac{S_{ABD}}{S_{ABC}}\)= \(\frac{m}{n+m}\) => \(S_{ABM}\)= \(\frac{1}{2}\) \(S_{ABC}\).
Giả sử AB < AC( m<n) vì AD là đường phân giác, AM là đường trung tuyến kẻ từ A nên AD nằm giữa AB và AM.
=> \(S_{ADM}\)= \(S_{ABM}\) - \(S_{ABD}\)
=> \(S_{ADM}\) = \(\frac{1}{2}\)S -\(\frac{m}{n+m}\)S = \(\frac{S(m+n-2m)}{2(m+n)}\)
\(S_{ADM}\)= \(\frac{S(n -m)}{2(m+n)}\) (với n>m)
