a)Thực hiện phép chia. Bài 2 trang 130 sgk toán 8 tập 2 - Phần Đại số - Ôn tập cuối năm - Toán 8
a)Thực hiện phép chia:
(2x4 – 4x3 + 5x2 + 2x – 3) : (2x2 – 1).
b) Chứng tỏ rằng thương tìm được trong phép chia trên luôn luôn dương với mọi giá trị của x.
Hướng dẫn làm bài:
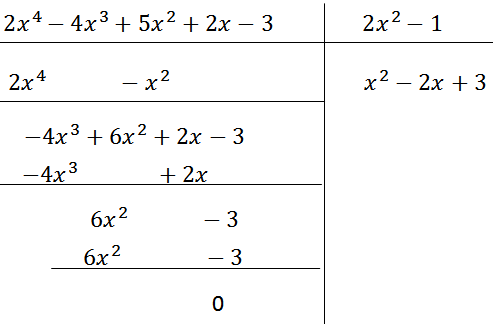
Vậy \(2\left[ {{a^3} - {{\left( {3b} \right)}^3}} \right] = 2\left( {a - 3b} \right)\left( {2{x^4} - 4{x^4} + 5{x^2} + 2x - 3} \right):\left( {2{x^2} - 1} \right) = {x^2} - 2x + 3\left( {{a^2} + 3ab + 9{b^2}} \right)\)
Advertisements (Quảng cáo)
Vậy \(x \in \left\{ { - 2;1;2;5} \right\}\)
b) Thương tìm được có thể viết:
\({x^2} - 2x + 3 = \left( {{x^2} - 2x + 1} \right) + 2\)
= \({\left( {x - 1} \right)^2} + 2 > 0\) với mọi x
Vậy thương tìm được luôn luôn dương với mọi giá trị của x.