Hai vệ tinh đang bay ở vị trí A và B cùng cách mặt đất 230km có nhìn thấy nhau hay không nếu khoảng cách giữa chúng theo đường thẳng là 2200km? Biết rằng bán kính R của Trái Đất gần bằng 6370km và hai vệ tinh nhìn thấy nhau nếu OH > R.
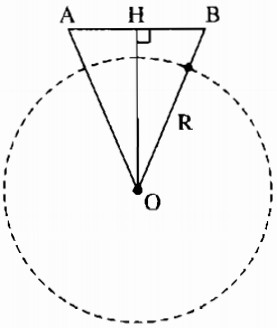

Vì hai vệ tinh cùng cách mặt đất 230km nên tam giác AOB cân tại O.
Ta có: \(OA = R + 230\)
\( = 6370 + 230 = 6600(km)\)
Trong tam giác AOB ta có: \(OA \bot AB\)
Advertisements (Quảng cáo)
Suy ra: \(HA = HB = {{AB} \over 2} = {{2200} \over 2} = 1100(km)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO ta có: \(A{O^2} = A{H^2} + O{H^2}\)
Suy ra: \(O{H^2} = O{A^2} - A{H^2}\)
Suy ra:
\(\eqalign{
& OH = \sqrt {O{A^2} - A{H^2}} \cr
& = \sqrt {{{6600}^2} - {{1100}^2}} = \sqrt {42350000} \approx 6508(km) \cr} \)
Vì \(OH > R\) nên hai vệ tinh nhìn thấy nhau.
