Cho tam giác ABC vuông tại A, đường cao AH (h.5).
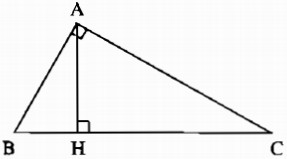
Giải bài toán trong mỗi trường hợp sau:
a) Cho AH = 16, BH = 25. Tính AB, AC, BC, CH;
b) Cho AB = 12, BH = 6. Tính AH, AC, BC, CH.

a) Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có: \({H^2} = BH.CH\)
\( \Rightarrow CH = {{A{H^2}} \over {BH}} = {{{{16}^2}} \over {25}} = 10,24\)
\(BC = BH + CH = 25 + 10,24 = 35,24\)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
Advertisements (Quảng cáo)
\(\eqalign{
& A{B^2} = BH.BC \cr
& \Rightarrow AB = \sqrt {BH.BC} \cr
& = \sqrt {25.35,24} = \sqrt {881} = 29,68 \cr} \)
\(\eqalign{
& A{C^2} = HC.BC \cr
& \Rightarrow AC = \sqrt {CH.BC} \cr
& = \sqrt {10,24.35,24} = \sqrt {360,9} = 18,99 \cr} \)
b) Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(\eqalign{
& A{B^2} = BH.BC \cr
& \Rightarrow BC = {{A{B^2}} \over {BH}} = {{{{12}^2}} \over 6} = 24 \cr} \)
\(CH = BC - BH = 24 - 6 = 18\)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(\eqalign{
& A{C^2} = HC.BC \cr
& \Rightarrow AC = \sqrt {CH.BC} \cr
& = \sqrt {18.24} = \sqrt {432} \approx 20,78 \cr} \)
Theo hệ thức liên hệ giữa đường cao và hình chiếu cạnh góc vuông, ta có:
\(\eqalign{
& A{H^2} = HB.HC \cr
& \Rightarrow AH = \sqrt {HB.HC} \cr
& = \sqrt {6.18} = \sqrt {108} = 6\sqrt 3 \cr} \)
