Cạnh huyền của một tam giác vuông lớn hơn một cạnh góc vuông là 1cm và tổng của hai cạnh góc vuông lớn hơn cạnh huyền 4cm. Hãy tính các cạnh của tam giác vuông này.

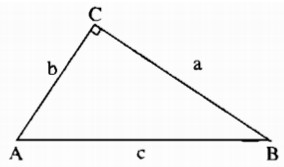
Giả sử tam giác ABC có \(\widehat {BAC} = 90^\circ \)
Theo đề bài, ta có: \(BC - AB = 1(cm)\) (1)
\(AB + AC - BC = 4(cm)\) (2)
Advertisements (Quảng cáo)
Từ (1) và (2) suy ra: \(BC - AB + AB + AC - BC = 4 + 1 = 5(cm)\)
Theo định lý Pi-ta-go, ta có: \(B{C^2} = A{B^2} + A{C^2}\) (3)
Từ (1) suy ra: \(BC = AB + 1\) (4)
Thay (4) và (3) ta có:
\(\eqalign{
& {\left( {AB + 1} \right)^2} = A{B^2} + A{C^2} \cr
& \Leftrightarrow A{B^2} + 2AB + 1 = A{B^2} + {5^2} \cr
& \Leftrightarrow 2AB = 24 \cr
& \Leftrightarrow AB = 12\left( {cm} \right) \cr} \)
Thay AB = 12 (cm) vào (1) ta có: \(BC = 12 + 1 = 13(cm)\)
