
Cho đường tròn (O) đường kính AB. Từ điểm M khác điểm A trên tiếp tuyến với đường tròn tại A, ta vẽ cát tuyến MCD (C nằm giữa M và D). Vẽ tiếp tuyến MI tiếp xúc với (O) tại I. Đường thẳng BC và BD cắt đường thẳng OM tại E và F. Chứng minh:
a) MICE là tứ giác nội tiếp.
b) O là trung điểm của EF.
a) Chứng minh tứ giác MICE có tổng hai góc đối bằng 1800.
b) Gọi G là giao điểm của AF và đường tròn \(\left( O \right)\), chứng minh BC//AG và O là trung điểm của CG. Áp dụng định lí Ta-lét.

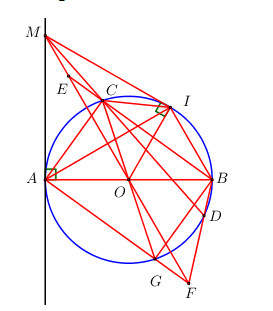
a) Ta có \(OA = OI = R \Rightarrow O\) thuộc trung trực của AI.
\(MA = MI\) (tính chất 2 tiếp tuyến cắt nhau) \( \Rightarrow \) M thuộc trung trực của AI.
Advertisements (Quảng cáo)
\( \Rightarrow OM\) là trung trực của AI \( \Rightarrow OM \bot AI\).
Ta có : \(\widehat {AIB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow IB \bot AI\)
\( \Rightarrow OM//IB \Rightarrow \widehat {IBC} = \widehat {CEO}\) (hai góc so le trong bằng nhau).
Lại có \(\widehat {IBC} = \widehat {CIM}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung IC)
\( \Rightarrow \widehat {CEO} = \widehat {CIM}\)\(\left( { = \widehat {IBC}} \right)\).
Mà \(\widehat {CEO} + \widehat {CEM} = {180^0}\) (hai góc kề bù) \( \Rightarrow \widehat {CIM} + \widehat {CEM} = {180^0} \Rightarrow \)Tứ giác MICE là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Gọi G là giao điểm của AF và đường tròn \(\left( O \right)\). Xét tứ giác ACBG nội tiếp đường tròn \(\left( O \right)\) có \(\widehat {ABC} = \widehat {AGC}\) (hai góc nội tiếp cùng chắn cung AC).
Mà tam giác OAG cân tại O (do \(OA = OG\)) \( \Rightarrow \widehat {AGC} = \widehat {OAG} \Rightarrow \widehat {ABC} = \widehat {OAG}\).
Ta có: \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ABC\) vuông tại C \( \Rightarrow \widehat {ABC} + \widehat {BAC} = {90^0}\)
\( \Rightarrow \widehat {OAG} + \widehat {BAC} = {90^0} \Rightarrow \widehat {CAG} = {90^0} \Rightarrow AG \bot AC\). Mà \(AC \bot BC\,\,\left( {\widehat {ACB} = {{90}^0}} \right) \Rightarrow AG//BC\).
Và \(\widehat {CAG}\) nội tiếp chắn nửa đường tròn \( \Rightarrow O\) là trung điểm của CG \( \Rightarrow OC = OG\)
Áp dụng định lí Ta-lét ta có: \(\dfrac{{OE}}{{OF}} = \dfrac{{OC}}{{OG}} = 1 \Rightarrow OE = OF\). Vậy O là trung điểm của EF.
