
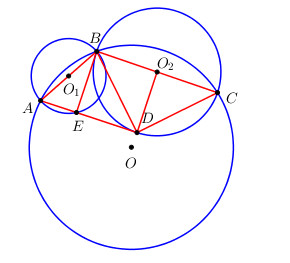
Gọi A, B, C là ba điểm theo thứ tự trên một đường thẳng. Vẽ hai đường tròn đường kính AB và BC. Từ A vẽ các đường thẳng tiếp xúc với đường tròn đường kính BC tại D và cắt đường tròn đường kính AB tại E. Chứng minh BD là phân giác góc \(\widehat {EBC}\).
Chứng minh \(\widehat {EBD}\) và \(\widehat {{O_2}BD}\) cùng bằng \(\widehat {{O_2}DB}\).

Advertisements (Quảng cáo)
Gọi O1 và O2 lần lượt là tâm đường tròn đường kính AB và đường tròn đường kính BC.
Xét đường tròn đường kính AB có \(\widehat {AEB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow AE \bot BE\)
Vì AD là tiếp tuyến của đường tròn đường kính BC tại D nên \({O_2}D \bot AD\) hay \({O_2}D \bot AE\)
Từ đó suy ra \({O_2}D//BE\) (cùng vuông góc với AE) \( \Rightarrow \widehat {EBD} = \widehat {{O_2}DB}\) (1) (so le trong)
Mà \({O_2}B = {O_2}D \Rightarrow \Delta {O_2}BD\) cân tại O2\( \Rightarrow \widehat {{O_2}DB} = \widehat {{O_2}BD}\) (2).
Từ (1) và (2) \( \Rightarrow \widehat {EBD} = \widehat {{O_2}BD} \Rightarrow BD\) là phân giác của góc \(\widehat {EBC}\) (đpcm).
