
Từ một điểm M bên ngoài đường tròn (O) vẽ hai tiếp tuyến MB, MC. Vẽ đường kính BOD. Hai đường thẳng CD và MB cắt nhau tại A. Chứng minh rằng M là trung điểm của AB.
+) Sử dụng tính chất hai tiếp tuyến cắt nhau \( \Rightarrow MB = MC\).
+) Chứng minh \(\widehat {MAC} = \widehat {MCA} \Rightarrow \Delta MAC\) cân tại M \( \Rightarrow MA = MC\).

Advertisements (Quảng cáo)
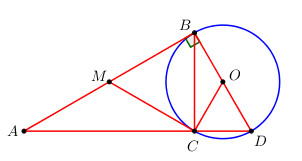
Do \(MB = MC\) (*) (tính chất hai tiếp tuyến cắt nhau) nên \(\Delta MBC\) cân tại M \( \Rightarrow \widehat {MBC} = \widehat {MCB}\) (1) (hai góc ở đáy).
Ta có: \(\widehat {BCD} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow BC \bot CD\) hay \(BC \bot AD \Rightarrow \Delta ABC\) vuông tại C.
\( \Rightarrow \widehat {MAC} + \widehat {MBC} = {90^0}\) (2) (hai góc nhọn trong tam giác vuông phụ nhau).
Lại có: \(\widehat {MCA} + \widehat {MCB} = \widehat {ACB} = {90^0}\) (3)
Từ (1), (2) và (3) \( \Rightarrow \widehat {MAC} = \widehat {MCA} \Rightarrow \Delta MAC\) cân tại M \( \Rightarrow MA = MC\) (**).
Từ (*) và (**) \( \Rightarrow MA = MB\). Lại có \(M \in AB \Rightarrow M\) là trung điểm của AB.
