
Tìm góc tạo bởi đường thẳng \(y = \sqrt 3 x - 1\) và trục Ox.
Vẽ đường thẳng trên hệ trục tọa độ Oxy, sau đó tính góc dựa vào hệ thức lượng trong tam giác vuông.

Giao của đường thẳng với trục Oy là điểm \(A\left( {0; - 1} \right)\)
Advertisements (Quảng cáo)
Giao của đường thẳng với trục Ox là điểm \(B\left( {\dfrac{1}{{\sqrt 3 }};0} \right)\)
Đồ thị cần tìm là đường thẳng đi qua 2 điểm A, B như hình vẽ
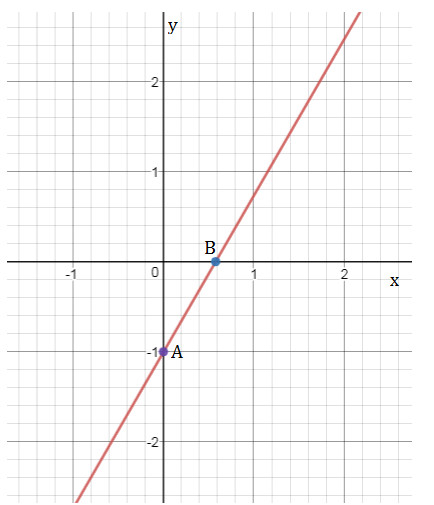
Xét tam giác vuông OAB ta có: \(OB = \left| {\dfrac{1}{{\sqrt 3 }}} \right| = \dfrac{1}{{\sqrt 3 }};OA = \left| { - 1} \right| = 1\) . Khi đó ta có: \(\tan \widehat {OBA} = \dfrac{{OA}}{{OB}} = \dfrac{1}{{\dfrac{1}{{\sqrt 3 }}}} = \sqrt 3 \Rightarrow \widehat {OBA} = {60^0}\)
Vậy góc tạo bởi đường thẳng \(y = \sqrt 3 x - 1\) và trục Ox là 600
