
Chứng minh \(\widehat {OAB} = \widehat {OBA} = \widehat {OCD} = \widehat {ODC} = \widehat {ODE} = \widehat {ODE} = \widehat {OEA} = \widehat {OAE}\)
Từ đó chứng minh nếu một ngũ giác nội tiếp và có các cạnh bằng nhau thì nó có phải là ngũ giác đều.
Chứng minh ngũ giác ABCDE có tất cả các góc bằng nhau.

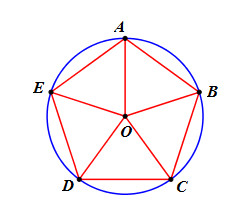
Ta có : \(AB = BC = CD = DE = EA \Rightarrow cung\,AB = cung\,BC = cung\,CD = cung\,DE = cung\,EA\) (các dây bằng nhau căng các cung bằng nhau).
Advertisements (Quảng cáo)
\( \Rightarrow \widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA}\) (số đo góc ở tâm bằng số đo cung bị chắn).
Xét \(\Delta OAB\) có \(OA = OB = R \Rightarrow \Delta OAB\) cân tại O.
\( \Rightarrow \widehat {OAB} = \widehat {OBA} = \dfrac{{{{180}^0} - \widehat {OAB}}}{2}\).
Chứng minh tương tự ta có
\(\begin{array}{l}\widehat {OBC} = \widehat {OCB} = \dfrac{{{{180}^0} - \widehat {BOC}}}{2}\\\widehat {OCD} = \widehat {ODC} = \dfrac{{{{180}^0} - \widehat {COD}}}{2}\\\widehat {ODE} = \widehat {ODE} = \dfrac{{{{180}^0} - \widehat {DOE}}}{2}\\\widehat {OEA} = \widehat {OAE} = \dfrac{{{{180}^0} - \widehat {EOA}}}{2}\end{array}\)
Mà \(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOA}\)
\(\begin{array}{l} \Rightarrow \widehat {OAB} = \widehat {OBA} = \widehat {OCD} = \widehat {ODC} = \widehat {ODE} = \widehat {ODE} = \widehat {OEA} = \widehat {OAE}\\ \Rightarrow \widehat {EAB} = \widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA}\end{array}\)
Vậy ngũ giác ABCDE là ngũ giác đều (Ngũ giác có tất cả các cạnh bằng nhau và các góc bằng nhau).
