
Một đa giác đều có n cạnh, đội dài mỗi cạnh là a. Hãy tính bán kính R và r của các đường tròn ngoại tiếp và nội tiếp đa giác đó theo a.
Tính \(\widehat {COD}\), sau đó tính sin \(\widehat {COB}\) và tan \(\widehat {COB}\), từ đó tính được R và r.

Advertisements (Quảng cáo)
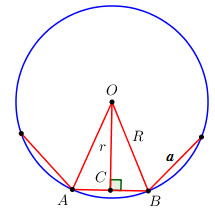
Giả sử một đa giác đều n cạnh có độ dài một cạnh là a. Gọi R là bán kính đường tròn ngoại tiếp, r bán kính đường tròn nội tiếp\( \Rightarrow OB = R;\,\,OC = r\)
\(\widehat {AOB} = \dfrac{{{{360}^0}}}{n} \Rightarrow \widehat {COB} = \dfrac{{{{360}^0}}}{n}:2 = \dfrac{{{{180}^0}}}{n}\)
Trong\(\Delta COB\) ta có:\(\widehat {OCB} = {90^0}\)
\(\begin{array}{l}\sin \widehat {COB} = \dfrac{{CB}}{{OB}} = \dfrac{{\dfrac{a}{2}}}{R} = \dfrac{a}{{2R}} \Rightarrow 2R = \dfrac{a}{{\sin \widehat {COB}}} = \dfrac{a}{{\sin \dfrac{{{{180}^0}}}{n}}} \Rightarrow R = \dfrac{a}{{2\sin \dfrac{{{{180}^0}}}{n}}}\\\tan \widehat {COB} = \dfrac{{CB}}{{OC}} = \dfrac{{\dfrac{a}{2}}}{r} = \dfrac{a}{{2r}} \Rightarrow 2r = \dfrac{a}{{\tan \widehat {COB}}} = \dfrac{a}{{\tan \dfrac{{{{180}^0}}}{n}}} \Rightarrow r = \dfrac{a}{{2\tan \dfrac{{{{180}^0}}}{n}}}\end{array}\)
