Bài tập - Chủ đề 2 : Góc chắn cung - Bài 15 trang 95 Tài liệu dạy – học Toán 9 tập 2. Giải bài tập Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ tiếp tuyến AB và cát tuyến ACD đi qua tâm O
Từ một điểm A ở bên ngoài đường tròn (O) ta vẽ tiếp tuyến AB và cát tuyến ACD đi qua tâm O (C nằm giữa A và D). Giả sử số đo của cung nhỏ BC bằng \({50^o}\) , hãy tính số đo góc A.
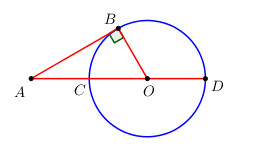
Vì \(\widehat {BOC}\) là góc ở tâm chắn cung BC BC \( \Rightarrow \widehat {BOC} = sd\,cung\,BC = {50^0}\)
Advertisements (Quảng cáo)
Vì AB là tiếp tuyến của đường tròn \(\left( O \right)\) tại B \( \Rightarrow AB \bot OB \Rightarrow \Delta OAB\) vuông tại B.
\( \Rightarrow \widehat A + \widehat {BOC} = {90^0}\) (tính chất hai góc nhọn phụ nhau trong tam giác vuông)
\( \Rightarrow \widehat A + {50^0} = {90^0} \Rightarrow \widehat A = {90^0} - {50^0} = {40^0}\).
Vậy \(\widehat A = {40^0}\).