
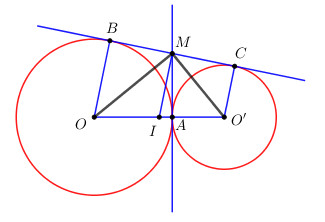
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài nhau tại A. Gọi M là giao điểm của một trong hai tiếp tuyến chung ngoài BC \(\left( {B \in \left( O \right),C \in \left( {O’} \right)} \right)\) và tiếp tuyến chung trong A. Chứng minh rằng BC là tiếp tuyến của đường tròn đường kính OO’ tại M.
+) Chứng minh \(IM \bot BC\), với \(I\) là trung điểm của \(OO’\).
+) Chứng minh \(M\) thuộc đường tròn đường kính \(OO’\).

Gọi \(I\) là trung điểm của \(OO’ \Rightarrow I\) là tâm đường tròn đường kính \(OO’\).
Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có: \(\left\{ \begin{array}{l}MA = MB\\MA = MC\end{array} \right. \Rightarrow MB = MC \Rightarrow M\) là trung điểm của \(BC\).
Vì \(BC\) là tiếp tuyến chung ngoài của \(\left( O \right)\) và \(\left( {O’} \right)\) nên \(\left\{ \begin{array}{l}OB \bot BC\\O’C \bot BC\end{array} \right. \Rightarrow OB//O’C \Rightarrow \) Tứ giác \(OBCO’\) là hình thang.
Advertisements (Quảng cáo)
Xét hình thang \(OBCO’\) có:
\(I\) là trung điểm của \(OO’\) (cách dựng)
\(M\) là trung điểm của \(BC\,\,\left( {cmt} \right)\)
\( \Rightarrow IM\) là đường trung bình của hình thang \(OBCO’ \Rightarrow IM//OB//O’C\).
Mà \(OB \bot BC \Rightarrow IM \bot BC\) tại \(M\) (1).
Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có:
\(MO\) là tia phân giác của \(\angle AMB\) ;
\(MO’\) là tia phân giác của \(\angle AMC\).
Mà \(\angle AMB\) và \(\angle AMC\) là 2 góc kề bù \( \Rightarrow MO \bot MO’ \Rightarrow \angle OMO’ = {90^0} \Rightarrow M\) thuộc đường tròn đường kính \(OO’\) (2).
Từ (1) và (2) \( \Rightarrow BC\) là tiếp tuyến của đường tròn đường kính \(OO’\).
Baitapsgk.com
