
Trên đường tròn (O ; R) cho hai điểm A, B. Hãy tính số đo các cung nhỏ và cung AB trong các trường hợp sau:
a) AB = R
b) AB = R\(\sqrt 2 \)
c) \(AB = R\sqrt 3 \)
a) Chứng minh tam giác OAB đều.
b, c) Gọi H là trung điểm của AB, sử dụng hàm số lượng giác sin, tính \(\widehat {AOH}\), từ đó suy ra \(\widehat {AOB}\) .

a) Xét tam giác OAB có \(OA = OB = OC = R \Rightarrow \Delta OAB\) đều .
b)
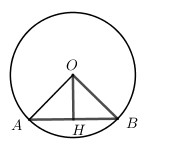
+) Gọi H là trung điểm của AB \( \Rightarrow OH \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung).
Ta có \(AH = BH = \dfrac{{AB}}{2} = \dfrac{{R\sqrt 2 }}{2}\).
Advertisements (Quảng cáo)
Xét tam giác vuông OAH có \(\sin \widehat {AOH} = \dfrac{{AH}}{{OA}} = \dfrac{{\dfrac{{R\sqrt 2 }}{2}}}{R} = \dfrac{{\sqrt 2 }}{2}\)
\(\Rightarrow \widehat {AOH} = {45^0}\).
Ta có \(OA = OB = R \Rightarrow \Delta OAB\) cân tại O \( \Rightarrow \) Đường cao OH đồng thời là phân giác
\( \Rightarrow \widehat {AOB} = 2\widehat {AOH} = {2.45^0} = {90^0}\)
\(\Rightarrow sd\,cung\,AB = {90^0}\).
c)
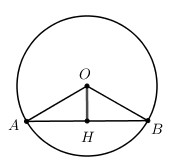
+) Gọi H là trung điểm của AB \( \Rightarrow OH \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung).
Ta có \(AH = BH = \dfrac{{AB}}{2} = \dfrac{{R\sqrt 3 }}{2}\).
Xét tam giác vuông OAH có \(\sin \widehat {AOH} = \dfrac{{AH}}{{OA}} = \dfrac{{\dfrac{{R\sqrt 3 }}{2}}}{R} = \dfrac{{\sqrt 3 }}{2}\)
\(\Rightarrow \widehat {AOH} = {60^0}\).
Ta có \(OA = OB = R \Rightarrow \Delta OAB\) cân tại O \( \Rightarrow \) Đường cao OH đồng thời là phân giác
\( \Rightarrow \widehat {AOB} = 2\widehat {AOH} = {2.60^0} = {120^0}\)
\(\Rightarrow sd\,cung\,AB = {120^0}\).
Baitapsgk.com
