Advertisements (Quảng cáo)
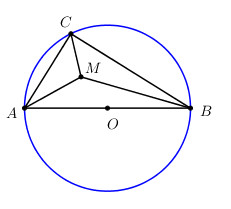
Cho đường tròn (O) đường kính AB và điểm C tùy ý trên đường tròn (O). Gọi M là giao điểm ba đường phân giác trong của tam giác ABC. Hỏi tập hợp các điểm M khi điểm C di động xung quanh đường tròn (O).
Chứng minh \(\widehat {AMB}\) không đổi.
Xét tam giác MAB có:
Advertisements (Quảng cáo)
\(\begin{array}{l}\widehat {AMB} + \widehat {MAB} + \widehat {MBA} = {180^0}\\ \Rightarrow \widehat {AMB} + \dfrac{1}{2}\widehat {CAB} + \dfrac{1}{2}\widehat {CBA} = {180^0}\\ \Leftrightarrow \widehat {AMB} + \dfrac{1}{2}\left( {\widehat {CAB} + \widehat {CBA}} \right) = {180^0}\end{array}\)
Ta có \(\widehat {ACB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta ABC\) vuông tại C \( \Rightarrow \widehat {CAB} + \widehat {CBA} = {90^0}\).
\( \Rightarrow \widehat {AMB} + \dfrac{1}{2}{.90^0} = {180^0} \)
\(\Leftrightarrow \widehat {AMB} = {135^0}\)
Do A, B cố định \( \Rightarrow \) Khi C di chuyển trên đường tròn \(\left( O \right)\) thì M di chuyển trên cung chứa góc 1350 dựng trên đoạn thẳng AB.
Baitapsgk.com