
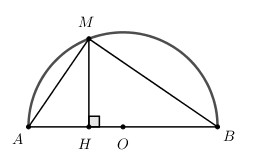
Cho nửa đường tròn đường kính AB = 2R. Gọi M là một điểm thuộc nửa đường tròn và H là hình chiếu của M trên AB. Hãy xác định vị trí của M để AH + HM đạt giá trị lớn nhất và tính giá trị lớn nhất đó theo R.
Áp dụng BĐT Bunhiacopxki: \({\left( {ax + by} \right)^2} \le \left( {{a^2} + {b^2}} \right)\left( {{x^2} + {y^2}} \right)\). Dấu “=” xảy ra \( \Leftrightarrow \dfrac{a}{x} = \dfrac{b}{y}\).

Advertisements (Quảng cáo)
Áp dụng BĐT Bunhiacopxki ta có:
\({\left( {AH + HM} \right)^2} \le 2\left( {A{H^2} + H{M^2}} \right) = 2A{M^2} \)
\(\Rightarrow AH + HM \le AM\sqrt 2 \).
Dấu “=” xảy ra \( \Leftrightarrow AH = HM\), khi đó tam giác AHM vuông cân tại H.
\( \Rightarrow \widehat {MAH} = {45^0} \Rightarrow \widehat {MAB} = {45^0}\).
Ta có \(\widehat {AMB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \Delta MAB\) vuông tại M. Mà \(\widehat {MAB} = {45^0} \Rightarrow \Delta MAB\) vuông cân tại M \( \Rightarrow MA = AB.\sin {45^0} = 2R.\dfrac{{\sqrt 2 }}{2} = R\sqrt 2 \).
Vậy \({\left( {AH + HM} \right)_{\max }} = AM\sqrt 2 \)\(\,= R\sqrt 2 .\sqrt 2 = 2R\).
Baitapsgk.com
