
Cho hai đường tròn đồng tâm có khoảng cách ngắn nhất giữa hai điểm thuộc hai đường tròn bằng 1m. Tính hiệu các chu vi của hai đường tròn.
Sử dụng công thức tính chu vi đường tròn bán kính R là \(2\pi R\).

Advertisements (Quảng cáo)
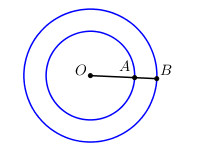
Lấy điểm A, B lần lượt thuộc 2 đường tròn sao cho O, A, B thẳng hàng.
Vì khoảng cách ngắn nhất giữa hai điểm thuộc hai đường tròn bằng 1m nên \(AB = 1m\).
Đặt \(OA = R \Rightarrow OB = OA + AB = R + 1\).
Chu vi đường tròn tâm O, bán kính OA là \({C_1} = 2\pi OA = 2\pi R\).
Chu vi đường tròn tâm O, bán kính OB là \({C_2} = 2\pi OB = 2\pi \left( {R + 1} \right) = 2\pi R + 2\pi \).
Vậy hiệu các chu vi của 2 đường tròn là \({C_2} - {C_1} = 2\pi R + 2\pi - 2\pi R = 2\pi \).
