
Cho tứ giác ABCD có AB = AC = AD = 20 cm, góc B bằng \({60^o}\) và góc A bằng \({90^o}\).
a) Tính đường chéo BD.
b) Tính khoảng cách BH và DK từ hai điểm B và D đến AC.
c) Vẽ BE vuông góc với DC kéo dài. Tính BE, CE, DC.
a) Áp dụng định lý Pythagore vào tam giác ABD vuông tại A để tính BD
b) Tính góc BAC và CAD từ dữ kiện đề bài từ đó sử dụng các hệ thức lượng giác để tính.
c) Tính góc BCE từ đó sử dụng các hệ thức lượng giác để tính BE, CE. Sử dụng định lý Pythagore tính ED từ đó suy ra CD.

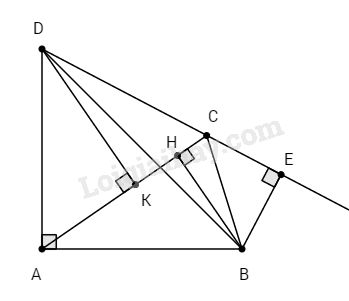
a) Tính đường chéo BD.
Áp dụng định lý Pythagore vào tam giác ABD vuông tại A:
\(B{D^2} = A{B^2} + A{D^2}\)\(\, = {20^2} + {20^2} = {2.20^2}\)
\(\Rightarrow BD = 20\sqrt 2 \) (cm)
b) Tính khoảng cách BH và DK từ hai điểm B và D đến AC.
Ta có AC = AB (gt) \( \Rightarrow \)\(\Delta \) ABC cân tại A mà góc B bằng \({60^o}\) \( \Rightarrow \)\(\Delta \) ABC đều
\( \Rightarrow \)\(\widehat {BAC} = {60^o}\)
Xét \(\Delta \)BHA vuông tại H, ta có:
\(\sin \left( {\widehat {BAC}} \right) = \dfrac{{BH}}{{AB}}\)
\(\Rightarrow BH = AB.\sin \left( {\widehat {BAC}} \right) \)\(\,= 20.\sin {60^o} = 10\sqrt 3 \) (cm)
Advertisements (Quảng cáo)
Lại có \(\widehat {BAC} + \widehat {CAD} = \angle BAD\)
\(\Rightarrow \widehat{ CAD }= \widehat {BAD} - \widehat {BAC} \)\(\,= {90^o} - {60^o} = {30^o}\)
Xét \(\Delta \) DKA vuông tại K, ta có:
\(\sin \left( {\widehat {DAK}} \right) = \dfrac{{DK}}{{AD}}\)
\(\Rightarrow DK = AD.\sin \left( {\widehat {DAK}} \right)\)\(\, = 20.\sin {30^o} = 10\) (cm)
c) Vẽ BE vuông góc với DC kéo dài. Tính BE, CE, DC.
Ta có: AC = AD (gt) \( \Rightarrow \)\(\Delta \)ACD cân tại A \( \Rightarrow \)\(\widehat {ACD} = \widehat {ADC}\)
Theo định lý tổng 3 góc trong tam giác ACD có:
\(\widehat {DAC} + \widehat {ACD} + \widehat {ADC} = {180^o}\)hay \({30^o} + \widehat {ACD} + \widehat {ACD} = {180^o}\)
\(\Rightarrow \widehat {ACD} = {75^o}\)
Có \(\Delta \)ABC đều (cmt) \( \Rightarrow \)\(\widehat {ACB} = {60^o}\); BC = AB = AD = 20 cm
Lại có \(\widehat {ACD} + \widehat {ACB} + \widehat {BCE} = {180^o}\)
\(\Rightarrow \widehat {BCE} = {180^o} - \widehat {ACD} - \widehat {ACB}\)\(\, = {180^o} - {75^o} - {60^o} = {45^o}\)
\( \Rightarrow \Delta \)BEC vuông cân tại E.
Xét \(\Delta \)BEC vuông cân tại E, ta có:
\(\sin \left( {\widehat {BCE}} \right) = \dfrac{{BE}}{{BC}}\)
\(\Rightarrow BE = BC.\sin \left( {\widehat {BCE}} \right) \)\(\,= 20.\sin {45^o} = 10\sqrt 2 \) (cm)
CE = BE = \(10\sqrt 2 \) cm
Áp dụng định lý Pythagore vào tam giác BDE vuông tại E:
\(E{D^2} = B{D^2} - B{E^2}\)\(\, = {2.20^2} - {\left( {10\sqrt 2 } \right)^2} = 600 \)
\(\Rightarrow ED = 10\sqrt 6 \) (cm)
\( \Rightarrow CD = ED - EC = 10\sqrt 6 - 10\sqrt 2\)\(\, = 10\left( {\sqrt 6 - \sqrt 2 } \right)\) (cm)
