Bài 37 trang 82 môn Toán 9 tập 2, Bài 37. Cho đường tròn (O)...

Bài 37. Cho đường tròn \((O)\) và hai dây \(AB\), \(AC\) bằng nhau. Trên cung nhỏ \(AC\) lấy một điểm \(M\). Gọi \(S\) là giao điểm của \(AM\) và \(BC\). Chứng minh: \(\widehat {ASC}\)=\(\widehat {MCA}\)

Hướng dẫn giải:

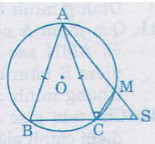
Ta có: \(\widehat {ASC}\)= \(\frac{sđ\overparen{AB}+sđ\overparen{MC}}{2}\)  (1)

(\(\widehat {ASC}\) là góc có đỉnh nằm bên ngoài đường tròn \((O)\))

và \(\widehat {MCA}\)=\(\frac{sđ\overparen{AM}}{2}\)   (2)

(góc nội tiếp chắn cung \(\overparen{AM}\))

Theo giả thiết thì:

     \(AB = AC =>\)\(\overparen{AB}=\overparen{AC}\)   (3)

Từ (1), (2), (3) suy ra: \(\overparen{AB}-\overparen{MC}=\overparen{AC}-\overparen{MC}=\overparen{AM}\)

Từ đó \(\widehat {ASC}=\widehat {MCA}\).