Cho điểm \(M(a; b)\) với \(a > 0, b > 0\). Viết phương trình đường thẳng qua \(M\) và cắt các tia \(Ox, Oy\) lần lượt tại \(A, B\) sao cho tam giác \(OAB\) có diện tích nhỏ nhất.

(h.95).
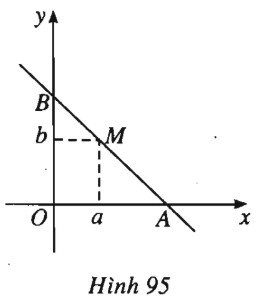
Gọi \(A(x_0 ; 0), B(0 ; y_0).\)
Khi đó, \(x_0 > 0, y_0 > 0\). Phương trình đường thẳng AB là \( \dfrac{x}{{{x_0}}} + \dfrac{y}{{{y_0}}} = 1\).
\(\begin{array}{l}M \in AB \Rightarrow \dfrac{a}{{{x_0}}} + \dfrac{b}{{{y_0}}} = 1.\\{S_{OAB}} = \dfrac{1}{2}.OA.OB = \dfrac{1}{2}{x_0}.{y_0}.\end{array}\)
Advertisements (Quảng cáo)
Ta có
\(1 = \dfrac{a}{{{x_0}}} + \dfrac{b}{{{y_0}}} \ge 2\sqrt { \dfrac{{ab}}{{{x_0}{y_0}}}}\)
\(\Rightarrow {x_0}{y_0} \ge 4ab\).
Do đó \({S_{OAB}} = \dfrac{1}{2}{x_0}{y_0} \ge \dfrac{1}{2}.4ab = 2ab\).
Dấu “=” xảy ra khi và chỉ khi \( \dfrac{a}{{{x_0}}} = \dfrac{b}{{{y_0}}} = \dfrac{1}{2}\) hay \(\left\{ \begin{array}{l}{x_0} = 2a\\{y_0} = 2b\end{array} \right.\).
Vậy diện tích tam giác \(OAB\) nhỏ nhất bằng 2ab khi \(\left\{ \begin{array}{l}{x_0} = 2a\\{y_0} = 2b\end{array} \right.\). Phương trình đường thẳng cần tìm là \( \dfrac{x}{{2a}} + \dfrac{y}{{2b}} = 1\).
