Cho hai đường thẳng
\({d_1}: 2x - y - 2 = 0 ,\)
\({d_2}: x + y + 3 = 0\) và điểm \(M(3 ; 0).\)
a) Tìm tọa độ giao điểm của \(d_1\) và \(d_2\).
b) Viết phương trình đường thẳng \(\Delta \) đi qua \(M\) , cắt \(d_1\) và \(d_2\) lần lượt tại điểm \(A\) và \(B\) sao cho \(M\) là trung điểm của đoạn thẳng \(AB.\)

a) Tọa độ giao điểm của hai đường thẳng \(d_1, d_2\) là nghiệm của hệ
\(\left\{ \begin{array}{l}2x - y - 2 = 0 \\ x + y + 3 = 0\end{array} \right.\)
Giải hệ ta có \(\left\{ \begin{array}{l}x = \dfrac{{ - 1}}{3}\\y = - \dfrac{8}{3}\end{array} \right.\)
b) (h.96).
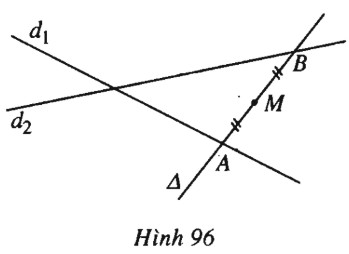
Cách 1:
\(A({x_A} ; {y_A}) \in {d_1} \Rightarrow {y_A} = 2{x_A} - 2 ;\) \( B({x_B} ; {y_B}) \in {d_2} \Rightarrow {y_B} = - {x_B} - 3\).
Vì \(M\) là trung điểm của \(AB\) nên
Advertisements (Quảng cáo)
\(\begin{array}{l}\left\{ \begin{array}{l}{x_A} + {x_B} = 2{x_M}\\{y_A} + {y_B} = 2{y_M} \end{array} \right. \\ \Rightarrow \left\{ \begin{array}{l}{x_A} + {x_B} = 6\\2{x_A} - 2 - {x_B} - 3 = 0\end{array} \right. \\ \Rightarrow {x_A} = \dfrac{{11}}{3} \Rightarrow {y_A} = \dfrac{{16}}{3}.\end{array}\)
Vậy \(A\left( { \dfrac{{11}}{3} ; \dfrac{{16}}{3}} \right)\).
Đường thẳng \(MA\) trùng với đường thẳng \(\Delta \). Từ đó ta tìm được phương trình của \(\Delta \) là \(8x-y-24=0.\)
Cách 2:
Dễ thấy đường thẳng \(\Delta \) cần tìm không vuông góc với \(Ox\). Gọi k là hệ số góc của \(\Delta \) thì phương trình của \(\Delta \) có dạng: \(y=k(x-3).\)
Gọi \(A = \Delta \cap {d_1} , B = \Delta \cap {d_2}\). Khi đó hoành độ của A là nghiệm của phương trình :\(2x - 2 = k(x - 3)\).
Suy ra \({x_A} = \dfrac{{3k - 2}}{{k - 2}} (k \ne 2\) vì nếu \(k=2\) thì phương trình \(2x - 2 = k(x - 3)\) vô nghiệm).
Hoành độ của \(B\) là nghiệm của phương trình \( - x - 3 = k(x - 3)\).
Suy ra \({x_B} = \dfrac{{3k - 3}}{{k + 1}} (k \ne - 1\) vì nếu \(k=-1\) thì phương trình \( - x - 3 = k(x - 3)\) vô nghiệm). Từ giả thiết \(M\) là trung điểm của \(AB\) suy ra:
\({x_A} + {x_B} = 2{x_M} \)
\( \Leftrightarrow \dfrac{{3k - 2}}{{k - 2}} + \dfrac{{3k - 3}}{{k + 1}} = 6 \Leftrightarrow k = 8\).
Vậy phương trình của \(\Delta \) là \(y=8(x-3)\) hay \(8x-y-24=0.\)
