Lập phương trình đường thẳng \(\Delta \) đi qua \(P(6 ; 4)\) và tạo với hai trục tọa độ một tam giác có diện tích bằng \(2\).

(h.94).
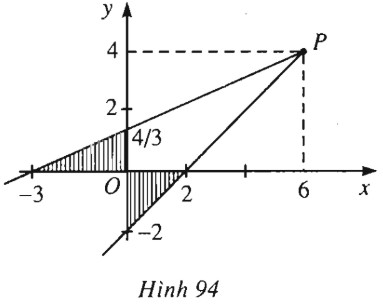
Giả sử \(\Delta \cap Ox = A(a ; 0) ,\) \( \Delta \cap Oy = B(0 ; b),\) \( a \ne 0, b \ne 0\).
Phương trình của \(\Delta \):\( \dfrac{x}{a} + \dfrac{y}{b} = 1\).
\(\begin{array}{l}P \in \Delta \Rightarrow \dfrac{6}{a} + \dfrac{4}{b} = 1 . (1)\\{S_{OAB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}|ab| = 2 \\ \Rightarrow |ab| = 4. (2)\end{array}.\)
Advertisements (Quảng cáo)
Từ (1) suy ra \(b = \dfrac{{4a}}{{a - 6}} (a \ne 6\) vì nếu \(a=6\) thì (1) trở thành \( \dfrac{4}{b} = 0\): vô lí ).
Thay vào (2) ta được \(\left| {a. \dfrac{{4a}}{{a - 6}}} \right| = 4 \Leftrightarrow {a^2} = |a - 6|\).
Vói \(a>6\) thì (3) \( \Leftrightarrow {a^2} - a + 6 = 0\) : phương trình vô nghiệm.
Vói \(a<6\) thì (3) \( \Leftrightarrow {a^2} + a - 6 = 0\), khi đó \(a=2\) hoặc \(a=-3.\)
- Trường hợp \(a = 2 \Rightarrow b = - 2\), ta có đường thẳng \({\Delta _1}: \dfrac{x}{2} + \dfrac{y}{{ - 2}} = 1\).
- Trường hợp \(a = - 3 \Rightarrow b = \dfrac{4}{3}\), ta có đường thẳng \({\Delta _2}: \dfrac{x}{{ - 3}} = \dfrac{y}{{ \dfrac{4}{3}}} = 1\).
