Cho tam giác \(ABC\) có \(A(0 ; 0),\) \( B(2 ; 4),\) \( C(6 ; 0)\) và các điểm \(M\) trên cạnh \(AB, N\) trên cạnh \(BC, P\) và \(Q\) trên cạnh \(AC\) sao cho \(MNPQ\) là hình vuông. Tìm tọa độ các điểm \(M, N, P, Q.\)

(h.97).
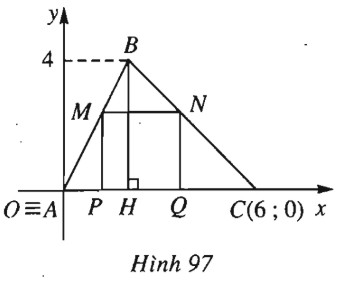
\(A(0 ; 0), C(6 ; 0) \Rightarrow A, C \in Ox \)
\( \Rightarrow P, Q \in Ox \)
\( \Rightarrow P = ({x_P} ; 0), Q = ({x_Q} ; 0)\) với \(0 < x_p < x_Q < 6.\)
Phương trình đường thẳng \(AB :y=2x;\)
Phương trình đường thẳng \(AC: y=0.\)
Advertisements (Quảng cáo)
Gọi cạnh hình vuông là \(a\). Ta có
\( \dfrac{{MN}}{{AC}} = \dfrac{{BM}}{{BA}} \Rightarrow \dfrac{a}{6} = \dfrac{{BM}}{{BA}}\) (1).
Kẻ \(BH \bot AC\), suy ra \(BH=4\). Ta có
\( \dfrac{{MP}}{{BH}} = \dfrac{{AM}}{{AB}} \Rightarrow \dfrac{a}{4} = \dfrac{{AM}}{{AB}} \) (2).
Từ (1) và (2) suy ra :\( \dfrac{a}{6} + \dfrac{a}{4} = \dfrac{{BM}}{{AB}} + \dfrac{{AM}}{{AB}} = 1\). Do đó \(a = \dfrac{{12}}{5}\).Vậy \({y_M} = {y_N} = \dfrac{{12}}{5}\).
Do \(M \in AB\) nên \({y_M} = 2{x_M}\), suy ra \({x_M} = \dfrac{6}{5}, {x_P} = {x_M} = \dfrac{6}{5}\).
Vì \(PQ = {x_Q} - {x_P}\) nên \({x_Q} = {x_P} + a = \dfrac{6}{5} + \dfrac{{12}}{5} = \dfrac{{18}}{5}\).
Các điểm cần tìm là \(M\left( { \dfrac{6}{5} ; \dfrac{{12}}{5}} \right), P\left( { \dfrac{6}{5} ; 0} \right), \) \( Q\left( { \dfrac{{18}}{5} ; 0} \right), N\left( { \dfrac{{18}}{5} ; \dfrac{{12}}{5}} \right)\).
