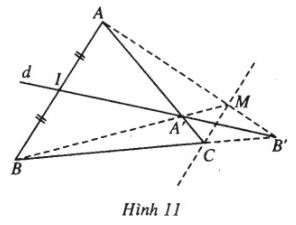
Cho tam giác \(ABC,\) \(I\) là trung điểm của đoạn thẳng \(AB\). Một đường thẳng d thay đổi luôn đi qua \(I\), lần lượt cắt hai đường thẳng \(CA\) và \(CB\) tại \(A’\) và \(B’\). Chứng minh rằng giao điểm \(M\) của \(AB’\) và \(A’B\) nằm trên một đường thẳng cố định.

(h.11)
Advertisements (Quảng cáo)
Đặt \(\overrightarrow {CB} = m\overrightarrow {CB’} \\,\,\overrightarrow {MB’} = n\overrightarrow {MA} \).
Xét tam giác \(ABB’\) với ba đường đồng quy là \(AC, BM, B’I\) ( đồng quy tại \(A’\)). Vì \(\overrightarrow {IA} = - \overrightarrow {IB} \) nên theo định lí Xê-va, ta có \(– mn = -1\) hay \(mn=1\). Từ \(\overrightarrow {MB’} = n\overrightarrow {MA} \) ta suy ra \(m\overrightarrow {MB’} = mn\overrightarrow {MA} = \overrightarrow {MA} \). Vậy ta có \(\overrightarrow {CB} = m\overrightarrow {CB’} \) và \(\overrightarrow {MA} = m\overrightarrow {MB’} \) điều này chứng tỏ rằng \(CM//AB\). Vậy điểm \(M\) luôn nằm trên đường thẳng cố định đi qua \(C\) và song song với \(AB\).
