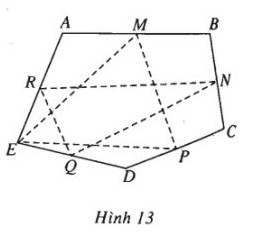
Cho ngũ giác \(ABCDE\). Gọi \(M, N, P, Q, R\) lần lượt là trung điểm các cạnh \(AB, BC, CD, DE, EA\). Chứng minh rằng hai tam giác \(MPE\) và \(NQR\) có cùng trọng tâm.

Với điểm \(G\) bất kì ta có
\(\eqalign{
& \overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GE} \cr
& = {1 \over 2}(\overrightarrow {GA} + \overrightarrow {GB} ) + {1 \over 2}(\overrightarrow {GC} + \overrightarrow {GD} ) + \overrightarrow {GE} \cr
& = {1 \over 2}(\overrightarrow {GB} + \overrightarrow {GC} ) + {1 \over 2}(\overrightarrow {GD} + \overrightarrow {GE} ) + {1 \over 2}(\overrightarrow {GE} + \overrightarrow {GA} ) \cr
& = \overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GR} \cr} \)
Advertisements (Quảng cáo)
Vậy \(\overrightarrow {GM} + \overrightarrow {GP} + \overrightarrow {GE} = \overrightarrow 0\)
\(\Leftrightarrow \,\,\,\overrightarrow {GN} + \overrightarrow {GQ} + \overrightarrow {GR} = \overrightarrow 0 \).
Suy ra trọng tâm hai tam giác \(MPE\) và \(NQR\) trùng nhau.
