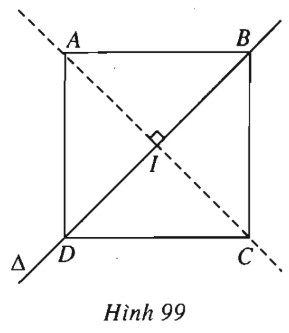
Lập phương trình các đường thẳng chứa bốn cạnh của hình vuông \(ABCD\) biết đỉnh \(A(-1 ; 2)\) và phương trình của một đường chéo là \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = - 2t\end{array} \right.\).

(h.99).
\(A \in \Delta : \left\{ \begin{array}{l}x = - 1 + 2t\\y = - 2t\end{array} \right.\).
Vậy \(B, D \in \Delta \). \(\Delta \) có vec tơ chỉ phương \(\overrightarrow u (2 ; - 2)\) nên phương trình đường chéo \(AC\) là
\(2(x + 1) - 2(y - 2) = 0\)
\(\Leftrightarrow x - y + 3 = 0\).
Tọa độ giao điểm \(I\) của \(AC\) và \(BD\) ứng với nghiệm t của phương trình:
\( - 1 + 2t + 2t + 3 = 0 \Leftrightarrow t = - \dfrac{1}{2}\).
Advertisements (Quảng cáo)
Vậy \(I=(-2 ; 1)\). Vì \(I\) là trung điểm của \(AC\) nên \(C=(-3 ; 0)\).
\(ABCD\) là hình vuông nên \(ID=IA=IB\). Do \(B \in \Delta \) nên \(B = ( - 1 + 2t ; - 2t)\).
\(\begin{array}{l}I{B^2} = I{A^2} \\\Leftrightarrow {( - 1 + 2t + 2)^2} + {( - 2t - 1)^2}\\ = {( - 1 + 2)^2} + {(2 - 1)^2}\\\Leftrightarrow {(2t + 1)^2} = 1\end{array}\)
\( \Leftrightarrow t = 0\) hoặc \(t = - 1\).
Suy ra \(B=(-1 ; 0)\) hoặc \(B=(-3 ; 2).\)
Nếu \(B=(-1 ; 0)\) thì \(D=(-3 ; 2),\) nếu \(B=(-3 ; 2)\) thì \(D=(-1 ; 0).\)
Đến đây, biết tọa độ bốn đỉnh của hình vuông \(ABCD\), ta sẽ dễ dàng viết được phương trình bốn cạnh của hình vuông là
\(x + 1 = 0 ; y = 0 ; \) \( x + 3 = 0 ; y - 2 = 0 .\)
