Cho hai đường thẳng \(\Delta : \left\{ \begin{array}{l}x = - 2t\\y = 1 + t\end{array} \right. , \Delta ‘: \left\{ \begin{array}{l}x = - 2 - t’\\y = t’\end{array} \right.\).
Viết phương trình đường thẳng đối xứng với \(\Delta \)’ qua \(\Delta \).

(h.100).
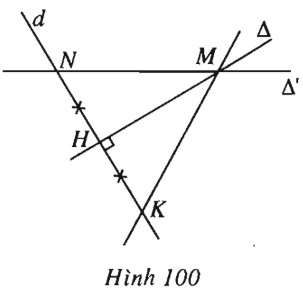
Dễ tìm được giao điểm \(M\) của \(\Delta \) và \(\Delta \)’ có tọa độ là \((-6 ; 4)\). Điểm \(N(-2 ; 0)\) thuộc \(\Delta \)’ và \(N\) khác \(M.\)
Advertisements (Quảng cáo)
Đường thẳng \(d\) đi qua \(N\) và vuông góc với \(\Delta \) có phương trình
\( - 2(x + 2) + y = 0 \Leftrightarrow 2x - y + 4 = 0\).
Gọi \(H = d \cap \Delta \), suy ra \(H = \left( { - \dfrac{6}{5} ; \dfrac{8}{5}} \right)\). Do đó tọa độ điểm \(K\) đối xứng với điểm \(N\) qua \(H\) là \(\left( { - \dfrac{2}{5} ; \dfrac{{16}}{5}} \right)\).
Đường thẳng cần tìm là đường thẳng \(MK\) và có phương trình \(x+7y-22=0.\)
