Cho hai hình bình hành \(ABCD\) và \(AB’C’D’\) có chung đỉnh \(A\). Chứng minh rằng
a) \(\overrightarrow {BB’} + \overrightarrow {C’C} + \overrightarrow {DD’} = \overrightarrow 0 \);
b) Hai tam giác \(BC’D\) và \(B’CD’\) có cùng trọng tâm.

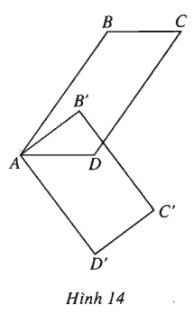
a) Ta có
\(\eqalign{ & \,\,\,\,\,\overrightarrow {BB’} + \overrightarrow {C’C} + \overrightarrow {DD’} \cr & = \overrightarrow {AB’} - \overrightarrow {AB} + \overrightarrow {AC} - \overrightarrow {AC’} + \overrightarrow {AD’} - \overrightarrow {AD} \cr & = (\overrightarrow {AD’} + \overrightarrow {AB’} ) - \overrightarrow {AC’} - (\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {AC} \cr & = \overrightarrow {AC’} - \overrightarrow {AC’} - \overrightarrow {AC} + \overrightarrow {AC} \cr & = \overrightarrow 0 \cr} \)
Advertisements (Quảng cáo)
b) Với điểm bất kì, ta có
\(\eqalign{ & \overrightarrow {GB} + \overrightarrow {GC’} + \overrightarrow {GD} \cr & = \overrightarrow {GB’} + \overrightarrow {B’B} + \overrightarrow {GC} + \overrightarrow {CC’} + \overrightarrow {GD’} + \overrightarrow {D’D} \cr & = \overrightarrow {GB’} + \overrightarrow {GC} + \overrightarrow {GD’} + (\overrightarrow {B’B} + \overrightarrow {CC’} + \overrightarrow {D’D} ) \cr & = \overrightarrow {GB’} + \overrightarrow {GC} + \overrightarrow {GD’} \cr} \)
Suy ra \(\overrightarrow {GB} + \overrightarrow {GC’} + \overrightarrow {GD} = \overrightarrow 0 \)
\(\Leftrightarrow \,\,\overrightarrow {GB’} + \overrightarrow {GC} + \overrightarrow {GD’} = \overrightarrow 0 \)
Vậy trọng tâm hai tam giác \(BC’D\) và \(B’CD’\) trùng nhau.
