Cho hình thang \(ABCD\) với các cạnh đáy là \(AB\) và \(CD\) (các cạnh bên không song song). Chứng minh rằng nếu cho trước một điểm \(M\) nằm giữa hai điểm hai điểm \(A, D\) thì có một điểm \(N\) nằm trên cạnh \(BC\) sao cho \(AN//MC\) và \(DN//MB.\)

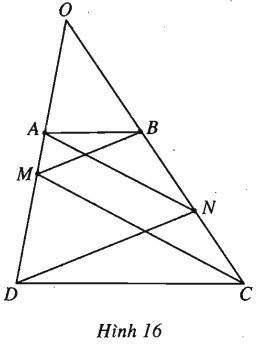
Gọi \(O\) là giao điểm của hai đường thẳng \(AD\) và \(BC\).
Đặt \(\overrightarrow {OA} = \overrightarrow a \,;\,\,\overrightarrow {OB} = \overrightarrow b \,\,;\,\,\,\overrightarrow {OD} = k\overrightarrow a \), khi đó \(\overrightarrow {OC} = k\overrightarrow b \) (vì \(AB//CD\)). Giả sử \(\overrightarrow {OM} = m\overrightarrow a \). Ta xác định điểm \(N\) trên \(BC\) sao cho \(AN//CM\). Ta chứng minh rằng \(DN//BM\).
Vì \(N\) nằm trên \(BC\) nên \(\overrightarrow {ON} = n\overrightarrow b \). Khi đó
\(\overrightarrow {AN} = \overrightarrow {ON} - \overrightarrow {OA} = n\overrightarrow b - \overrightarrow a \)
Mặt khác \(\overrightarrow {CM} = \overrightarrow {OM} - \overrightarrow {OC} = m\overrightarrow a - k\overrightarrow b \).
Advertisements (Quảng cáo)
Vì \(AN//CM\) nên hai vec tơ \(\overrightarrow {AN} \\,\,\overrightarrow {CM} \) cùng phương, tức là \(\dfrac{n}{{ - k}} = \dfrac{{ - 1}}{m}\) hay \(n = \dfrac{k}{m}\).
Vậy \(\overrightarrow {ON} = \dfrac{k}{m}\overrightarrow b \). Từ đó \(\overrightarrow {DN} = \overrightarrow {ON} - \overrightarrow {OD} = \dfrac{k}{m}\overrightarrow b - k\overrightarrow a \).
Lại có \(\overrightarrow {BM} = \overrightarrow {OM} - \overrightarrow {OB}\)
\( = m\overrightarrow a - \overrightarrow b\)
\( = - \dfrac{m}{k}\left( {\dfrac{k}{m}\overrightarrow b - k\overrightarrow a } \right)\)
\(= - \dfrac{m}{k}\overrightarrow {DN} \)
Vậy \(\overrightarrow {BM} \\,\,\overrightarrow {DN} \) cùng phương hay \(BM//DN.\)
