Cho tam giác \(ABC\). Lấy các điểm \(A’, B’, C’\) sao cho
\(\overrightarrow {A’B} = - 2\overrightarrow {A’C} ;\) \(\overrightarrow {B’C} = - 2\overrightarrow {B’A};\) \(\overrightarrow {C’A} = - 2\overrightarrow {C’B} \)
Đoạn thẳng \(AA’\) cắt các đoạn \(BB’\) và \(CC’\) lần lượt tại \(M\) và \(N\), hai đoạn \(BB’\) và \(CC’\) cắt nhau tại \(P\).
a) So sánh các đoạn thẳng \(AM, MN, NA’.\)
b) So sánh diện tích hai tam giác \(ABC, MNP.\)

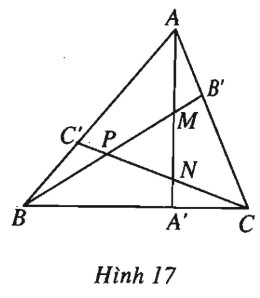
a) Đặt \(\overrightarrow {CA} = \overrightarrow a \,\,;\,\,\overrightarrow {CB} = \overrightarrow b \). Theo giả thiết ta có:
\(\overrightarrow {CA’} = \dfrac{{\overrightarrow {CB} }}{3} = \dfrac{{\overrightarrow b }}{3};\) \(\overrightarrow {CB’} = \dfrac{2}{3}\overrightarrow {CA} = \dfrac{{2\overrightarrow a }}{3};\) \(\overrightarrow {CC’} = \dfrac{{\overrightarrow {CA} + 2\overrightarrow {CB} }}{3} = \dfrac{{\overrightarrow a + 2\overrightarrow b }}{3}\)
Vì \(M\) là giao điểm của \(AA’\) và \(BB’\) nên có các số \(x\) và \(y\) sao cho :
\(\overrightarrow {CM} = x\overrightarrow {CA} + (1 - x)\overrightarrow {CA’}\)
\( = y\overrightarrow {CB} + (1 - y)\overrightarrow {CB’} \),
hay
\(x\overrightarrow a + (1 - x)\dfrac{{\overrightarrow b }}{3}\)
\(= y\overrightarrow b + (1 - y)\dfrac{{2\overrightarrow a }}{3}\).
Vì hai vec tơ \(\overrightarrow a \\,\,\overrightarrow b \) không cùng phương nên từ đẳng thức trên ta suy ra
Advertisements (Quảng cáo)
\(x = \dfrac{{2(1 - y)}}{3}\) và \(y = \dfrac{{1 - x}}{3}\).
Giaỉ ra ta được \(x = \dfrac{4}{7}\\,\,y = \dfrac{1}{7}\)
Từ đó ta có
\(\begin{array}{l}\overrightarrow {CM} = \dfrac{4}{7}\overrightarrow {CA} + \dfrac{3}{7}\overrightarrow {CA’} \\ \Rightarrow \dfrac{4}{7}\overrightarrow {MA} + \dfrac{3}{7}\overrightarrow {MA’} = \overrightarrow 0 \\ \Rightarrow \overrightarrow {MA} = - \dfrac{3}{4}\overrightarrow {MA’} \\\Rightarrow \,AM = \dfrac{3}{7}AA’\\\overrightarrow {CM} = \dfrac{1}{7}\overrightarrow {CB} + \dfrac{6}{7}\overrightarrow {CB’}\\ \Rightarrow \dfrac{1}{7}\overrightarrow {MB} + \dfrac{6}{7}\overrightarrow {MB’} = \overrightarrow 0 \\ \Rightarrow \overrightarrow {MB} = - 6\overrightarrow {MB’} \\\Rightarrow \,\,MB’ = \dfrac{1}{7}BB’\end{array}\)
Tương tự với \(MB’ = \dfrac{1}{7}BB’\) ta cũng có \(NA’ = \dfrac{1}{7}AA’\).
Vì \(AM = \dfrac{3}{7}AA’\) nên \(MN = \dfrac{3}{7}AA’\). Tóm lại, ta có \(AM=MN=3NA’.\)
Tương tự \(BP=PM=3MB’\) và \(CN=NP=3PC’.\)
b) Gọi \(S\) là diện tích tam giác \(ABC\). Từ giả thiết ta suy ra \(AB’ = \dfrac{1}{3}AC,\) \(CA’ = \dfrac{1}{3}CB,\) \(BC’ = \dfrac{1}{3}BA\).
Vậy ta có \({S_{ABB’}} = {S_{BCC’}} = {S_{CAA’}} = \dfrac{1}{3}S\).
Trong tam giác ABB’, ta có \(MB’ = \dfrac{1}{7}BB’\) nên \({S_{AB’M}} = \dfrac{1}{7}{S_{ABB’}} = \dfrac{1}{{21}}S\).
Tương tự: .
Từ đó suy ra
\(\begin{array}{l}{S_{MNP}} = {S_{ABC}} - {S_{ABB’}} - {S_{BCC’}}\\ - {S_{CAA’}} + {S_{AB’M}} + {S_{BC’P}} + {S_{CA’N}}\\ = S - 3.\dfrac{S}{3} + 3.\dfrac{1}{{21}}S = \dfrac{1}{7}S\end{array}\)
Vậy \({S_{ABC}} = 7{S_{MNP}}\).
