Cho hình vuông có đỉnh \(A=(-4 ; 5)\) và một đường chéo nằm trên đường thẳng có phương trình \(7x-y+8=0\). Lập phương trình các đường thẳng chứa các cạnh và đường chéo thứ hai của hình vuông.

(h.101).
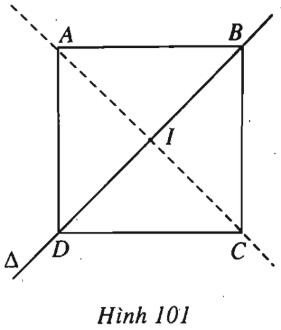
Nhận thấy \(A \notin \Delta : 7x - y + 8 = 0\). Vậy \(B, D \in \Delta \).
\(\Delta \) có vec tơ chỉ phương \(\overrightarrow u (1 ; 7)\). Phương trình đường chéo \(AC\) là:
\(1(x + 4) + 7(y - 5) = 0\)
\(\Leftrightarrow x + 7y - 31 = 0\).
Tọa độ giao điểm \(I\) của \(AC\) và \(BD\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}7x - y + 8 = 0\\x + 7y - 31 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{1}{2}\\y = \dfrac{9}{2}\end{array} \right.\). Vậy \(I\left( { - \dfrac{1}{2} ; \dfrac{9}{2}} \right)\)
Suy ra tọa độ của \(C\) là \((3 ; 4)\).
Vì \(ABCD\) là hình vuông nên \(AC\) tạo với các đường thẳng \(AB\) và \(AD\) các góc \(45^0\). Đường thẳng \(d\) đi qua \(A(-4 ; 5)\) có phương trình:
Advertisements (Quảng cáo)
\(\alpha (x + 4) + \beta (y - 5) = 0 \)
\(\Leftrightarrow \alpha x + \beta y + 4\alpha - 5\beta = 0\) \(({\alpha ^2} + {\beta ^2} \ne 0)\).
D tạo với \(AC\) một góc \(45^0\) khi và chỉ khi \(\cos {45^0} = \dfrac{{|\alpha + 7\beta |}}{{\sqrt {50.} \sqrt {{\alpha ^2} + {\beta ^2}} }}\)
\( \Leftrightarrow \dfrac{1}{{\sqrt 2 }} = \dfrac{{|\alpha + 7\beta |}}{{\sqrt {50} .\sqrt {{\alpha ^2} + {\beta ^2}} }}\)
\(\Leftrightarrow 12{\alpha ^2} - 7\alpha \beta - 12{\beta ^2} = 0\)
\(\Leftrightarrow \left[ \begin{array}{l}\alpha = \dfrac{4}{3}\beta \\\alpha = - \dfrac{3}{4}\beta \end{array} \right.\)
Với \(\alpha = \dfrac{4}{3}\beta \), ta chọn \(\beta = 3, \alpha = 4\) ta được đường thẳng \({d_1}: 4x + 3y + 1 = 0\).
Với \(\alpha = - \dfrac{3}{4}\beta \), ta chọn \(\beta = - 4, \alpha = 3\) ta được đường thẳng \({d_2}: 3x - 4y + 32 = 0\).
Lấy phương trình \(AB\) là :\(4x+3y+1=0\) thì phương trình \(AD\) là \(3x-4y+32=0.\)
Do đó ta viết được phương trình của \(CD\) và \(BC\) lần lượt là \(4x+3y-24=0\) và \(3x-4y+7=0.\) (Lấy phương trình \(AD\) là \(4x+3y+1=0\) thì phương trình của \(AB\) là \(3x-4y+32=0\) và ta cũng có kết quả tương tự).
