Bài 39 trang 106 SBT Hình học 10 Nâng cao. Cho tam giác \(ABC\) có đỉnh \(A = \left( { \dfrac{4}{5} ; \dfrac{7}{5}} \right)\). Hai đường phân giác trong của góc \(B\) và \(C\) lần lượt. Bài 3. Khoảng cách và góc.
Cho tam giác \(ABC\) có đỉnh \(A = \left( { \dfrac{4}{5} ; \dfrac{7}{5}} \right)\). Hai đường phân giác trong của góc \(B\) và \(C\) lần lượt có phương trình \(x-2y-1=0\) và \(x+3y-1=0\). Viết phương trình cạnh \(BC\) của tam giác .

(h.102).
Advertisements (Quảng cáo)
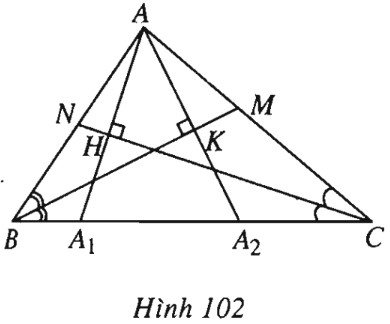
Kẻ \(AH \bot CN, AK \bot BM\). Gọi \(A_1, A_2\) theo thứ tự là giao điểm của \(AH, AK\) với \(BC\). Khi đó \(H\) là trung điểm của \(AA_1\), \(K\) là trung điểm của \(AA_2\). Ta tìm được tọa độ của \(A_1\) và \(A_2\). Từ đó viết được phương trình cạnh \(BC\) là \(y+1=0.\)
