Cho ba điểm \(A, B, C\) thẳng hàng, \(B\) nằm giữa \(A, C\) và đường thẳng \(\Delta \) qua \(A.\)
a) Chứng minh rằng có hai đường tròn cùng đi qua \(B, C\) và cùng tiếp xúc với \(\Delta \).
b) Chứng minh rằng khi \(\Delta \) quay quanh \(A\), các đường tròn đi qua \(B\) và hai tiếp điểm của \(\Delta \) với hai đường tròn ở câu a) luôn đi qua một điểm cố định khác \(B\).
Giải
(h.49).
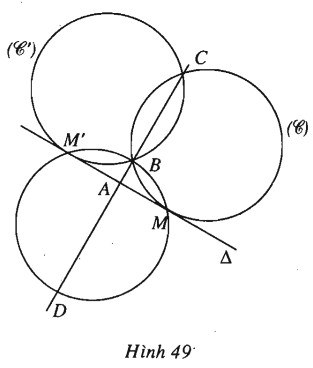
a) Gọi \(M\) là tiếp điểm của \(\Delta \) với đường tròn \((C)\) đi qua \(B\) và \(C,\) khi đó \(A{M^2} = \overrightarrow {AB} .\overrightarrow {AC} = AB.AC\) không đổi. Do đó \(M\) là giao điểm của \(\Delta \) và đường tròn tâm \(A\), bán kính bằng \(\sqrt {AB.AC} \).
Advertisements (Quảng cáo)
Từ đó suy ra có hai đường tròn cùng đi qua \(B, C\) và cùng tiếp với \(\Delta \).
b) Gọi \(M, M’\) là hai tiếp điểm của \(\Delta \) với hai đường tròn ở câu a) và gọi\(D\) là giao điểm (khác B) của đường thẳng \(BC\) với đường tròn \((BMM’)\) thì
\(\overrightarrow {AB} .\overrightarrow {AD} = \overrightarrow {AM} .\overrightarrow {AM’}\)
\( = - A{M^2} = - \overrightarrow {AB} .\overrightarrow {AC} .\)
Từ đó suy ra \(\overrightarrow {AD} = - \overrightarrow {AC} \) hay \(D\) là điểm đối xứng với \(C\) qua \(A\), do đó \(D\) là điểm cố định. Vậy khi \(\Delta \) quay quanh \(A\), các đường tròn \((BMM’)\) luôn đi qua điểm \(D\) cố định khác \(B.\)
