Cho tứ giác \(ABCD\) có các cạnh \(AB, CD\) kéo dài cắt nhau ở \(E\) và các cạnh \(AD, BC\) kéo dài cắt nhau ở \(F.\) Chứng minh rằng các trung điểm của các đoạn \(AC, BD\) và \(EF\) cùng thuộc một đường thẳng (đường thẳng Gao-xơ của tứ giác ).
Giải
(h.47).
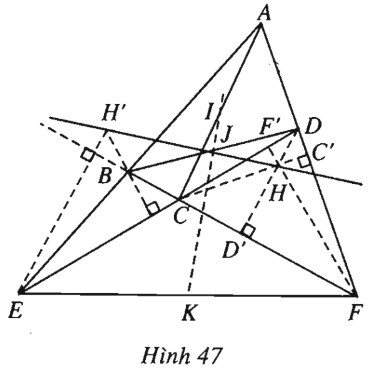
Kẻ các đường cao \(CC’, DD’, FF’\) của tam giác \(CDF\) và gọi \(H\) là trực tâm của tam giác đó thì
\(\overrightarrow {HC} .\overrightarrow {HC’} = \overrightarrow {HD} .\overrightarrow {HD’}\)
\( = \overrightarrow {HF} .\overrightarrow {HF’} \,\,\,\,(*)\)
Ta có trung điểm \(I\) của \(AC\) cũng la tâm đường tròn đường kính \(AC\), đường tròn đó đi qua \(C’\) (do \(\widehat {AC’C} = {90^0}\)).
Suy ra \({\wp _{H/(I)}} = \overrightarrow {HC} .\overrightarrow {HC’} \).
Advertisements (Quảng cáo)
Tương tự như vậy, \({\wp _{H/(J)}} = \overrightarrow {HD} .\overrightarrow {HD’} \) (\(J\) là tâm đường tròn đường kính \(BD\) ).
\({\wp _{H/(K)}} = \overrightarrow {HF} .\overrightarrow {HF’} \) (\(K\) là tâm đường tròn đường kính \(EF\) ).
Kết hợp với (*) suy ra
\({\wp _{H/(I)}} = {\wp _{H/(J)}} = {\wp _{H/(K)}}\).
Nếu lấy trực tâm \(H’\) của tam giác \(BCE\) ta cũng sẽ có
\({\wp _{H’/(I)}} = {\wp _{H’/(J)}} = {\wp _{H’/(K)}}\).
Vậy \(HH’\) là trục đẳng phương của hai đường tròn \((I)\) và \((J)\), nên \(HH’ \bot IJ\). \(HH’\) cũng là trục đẳng phương của \((I)\) và \((K)\), nên \(HH’ \bot IK\).
Từ đó ta có \(I, J, K\) thẳng hàng.
