Cho đường cong \((C_m)\) có phương trình:
\({x^2} + {y^2} + (m + 2)x - (m + 4)y + m + 1 = 0\)
a) Chứng minh rằng \((C_m)\) luôn là đường tròn với mọi giá trị của m.
b) Tìm tập hợp tâm các đường tròn \((C_m)\) khi m thay đổi.
c) Chứng minh rằng khi \(m\) thay đổi, họ các đường tròn \((C_m)\) luôn đi qua hai điểm cố định.
d) Tìm những điểm trong mặt phẳng tọa độ mà họ \((C_m)\) không đi qua dù m lấy bất cứ giá trị nào.

a) Phương trình \((C_m)\) có dạng \({x^2} + {y^2} + 2ax + 2by + c = 0\).
Với \(a = \dfrac{{m + 2}}{2} , b = - \dfrac{{m + 4}}{2} , c = m + 1\).
Ta có
\({a^2} + {b^2} - c\)
\(= {\left( { \dfrac{{m + 2}}{2}} \right)^2} + {\left( { \dfrac{{m + 4}}{2}} \right)^2} - (m + 1)\)
\(= \dfrac{{{m^2} + 4m + 8}}{2} > 0\) với mọi \(m.\)
Vậy \((C_m)\) là đường tròn với mọi giá trị của \(m.\)
b) Tọa độ tâm \(I_m\) của đường tròn \((C_m)\) là \(\left\{ \begin{array}{l}x = - \dfrac{{m + 2}}{2}\\y = \dfrac{{m + 4}}{2}\end{array} \right. \)
\(\Rightarrow \left\{ \begin{array}{l}2x = - (m + 2)\,\,\,\,\,\,\,\,\,\,(1)\\2y = m + 4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\end{array} \right.\)
Cộng từng vế của (1) và (2), ta được \(2x+2y=2\) hay \(x+y-1=0.\)
Advertisements (Quảng cáo)
Vậy tập hợp tâm của các đường tròn \((C_m)\) là đường thẳng có phương trình: \(x+y-1=0.\)
c) Gọi \(M(x_0 ;y_0)\) là điểm cố định mà họ \((C_m)\) luôn đi qua. Khi đó ta có
\(\begin{array}{l}x_0^2 + y_0^2 + (m + 2){x_0} - (m + 4){y_0} + m + 1 = 0 \,\,\,\,\,\forall m\\ \Leftrightarrow ({x_0} - {y_0} + 1)m + x_0^2 + y_0^2 + 2{x_0} - 4{y_0} + 1 = 0 \,\,\,\,\,\forall m\\ \Leftrightarrow \left\{ \begin{array}{l}{x_0} - {y_0} + 1 = 0\,\,\,\,\,\,\,\,\,\,(1)\\x_0^2 + y_0^2 + 2{x_0} - 4{y_0} + 1 = 0 \,\,\,\,\,\,\,\,\,\,(2)\end{array} \right.\end{array}\)
Từ (1) suy ra \(x_0=y_0-1,\) thay vào (2), ta được:
\({({y_0} - 1)^2} + y_0^2 + 2({y_0} - 1) - 4{y_0} + 1 = 0\)
\(\Leftrightarrow 2y_0^2 - 4{y_0} = 0 \Leftrightarrow \left[ \begin{array}{l}{y_0} = 0\\{y_0} = 2.\end{array} \right.\)
Với \(y_0=0\) thì \(x_0=-1\). Ta được điểm \(M_1(-1 ; 0).\)
Với \(y_0=2\) thì \(x_0=1.\) Ta được điểm \(M_1(1 ; 2).\)
Vậy họ đường tròn \((C_m)\) luôn đi qua hai điểm cố định là \(M_1(-1 ; 0)\) và \(M_2(1 ; 2).\)
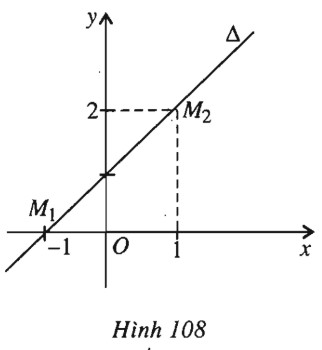
d) (h.108).
\((C_m)\) không đi qua điểm \((x_1 ; y_1)\) với mọi \(m\) khi và chỉ khi phương trình (ẩn \(m\)) :
\(({x_1} - {y_1} + 1)m + x_1^2 + y_1^2 + 2{x_1} - 4{y_1} + 1 = 0\) vô nghiệm
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{x_1} - {y_1} + 1 = 0\\x_1^2 + y_1^2 + 2{x_1} - 4{y_1} + 1 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{y_1} = {x_1} + 1\\{x_1} \ne \pm 1.\end{array} \right.\end{array}\)
Vậy tập hợp các điểm trong mặt phẳng tọa độ mà họ \((C_m)\) không bao giờ đi qua với mọi giá trị của \(m\) là đường thẳng \(\Delta \) có phương trình \(y=x+1\), bỏ đi hai điểm \(M_1(-1 ; 0)\) và \(M_2(1 ; 2).\)
