Cho đường tròn \((C): {(x - a)^2} + {(y - b)^2} = {R^2}\) và điểm \({M_0}({x_{0 }} ; {y_0}) \in (C)\). Chứng minh rằng tiếp tuyến \(\Delta \) của đường tròn \((C)\) tại \(M_0\) có phương trình:
\(({x_0} - a)(x - a) + ({y_0} - b)(y - b) = {R^2}\)

(h.106).
Advertisements (Quảng cáo)
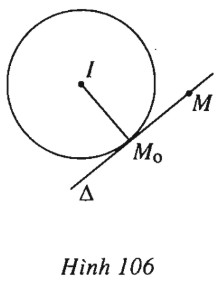
\((C)\) có tâm \(I(a, b)\), bán kính \(R\). Khi đó
\(\begin{array}{l}M(x ; y) \in \Delta \Leftrightarrow \overrightarrow {I{M_0}} .\overrightarrow {{M_0}M} = 0 \\\Leftrightarrow ({x_0} - a)(x - {x_0}) + ({y_0} - b)(y - {y_0}) = 0\\ \Leftrightarrow ({x_0} - a)(x - a + a - {x_0}) + ({y_0} - b)(y - b + b - {y_0}) = 0\\\Leftrightarrow ({x_0} - a)(x - a) + ({y_0} - b)(y - b) - [{({x_0} - a)^2} + {({y_0} - b)^2}] = 0\\\Leftrightarrow ({x_0} - a)(x - a) + ({y_0} - b)(y - b) = {R^2}\end{array}\)
