Advertisements (Quảng cáo)
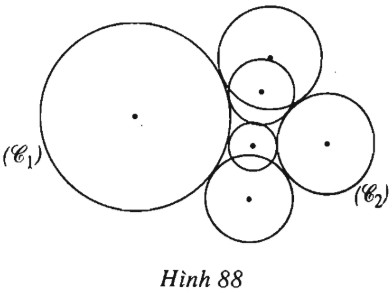
(h.88). Cho hai đường tròn \((C_1)\) và \((C_2)\) nằm ngoài nhau và có bán kính không bằng nhau. Chứng minh rằng tâm của các đường tròn cùng tiếp xúc ngoài hoặc cùng tiếp xúc trong với \((C_1)\) và \((C_2)\) nằm trên một hypebol với các tiêu điểm là tâm của các đường tròn \((C_1)\) và \((C_2)\). Tâm đối xứng của hypebol này nằm ở đâu ?
(h.114).
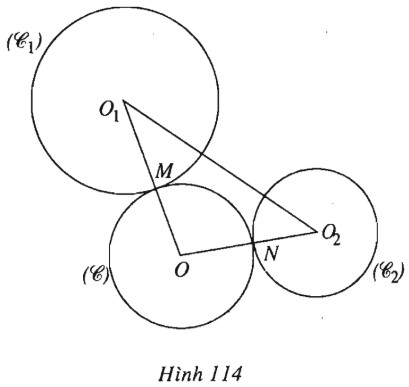
Kí hiệu \(O_1, R_1\) là tâm và bán kính của đường tron \((C_1); O_2, R_2\) là tâm và bán kính của đường tròn \((C_2).\)
Xét đường tròn thay đổi \((C)\), tâm \(O\), bán kính \(R\). \((C)\) tiếp xúc ngoài với \((C_1)\) tại \(M\), với \((C_2)\) tại \(N\). Ta có:
Advertisements (Quảng cáo)
\(|O{O_1} – O{O_2}| \)
\( = |(OM + {O_1}M) – (ON + {O_2}N)| \)
\(= |{O_1}M – {O_2}N| = |{R_1} – {R_2}| > 0\) (do \({R_1} \ne {R_2}\)).
Do đó \(O\) nằm trên một hypebol có các tiêu điểm là \(O_1\) và \(O_2\). Tâm đối xứng của hypebol này là trung điểm của \(O_1O_2\). Lập luận tương tự cho trường hợp đường tròn \((C)\) cùng tiếp xúc trong với các đường tròn \((C_1), (C_2).\)